目次
今年も開成を筆頭に高度な問題が多く出題
――今年はどんな特徴がありましたか?
川島 慶さん(以下、川島) 年々、問題が高度化する傾向があり、中学受験の算数の難しさとしていよいよ終着点を迎えたかなと思います。
――確かに難しいです。
川島 難関校が高度なテクニックや複雑な考え方を必要とする問題を出すと、翌年以降の受験生は、そういう問題に対する対策というか、パターン練習が必要になります。すると翌年、学校側はさらに新しく難しい問題を出す…と〝いたちごっこ〟の状態になり、年々高度化する傾向が続いていました。今年も、そういう意味では、例年通り、開成を筆頭に上位校で高度な問題が出されています。
――子どもたちの負担は大きいですね。
川島 その一方で、算数のおもしろさを凝縮しながらも、同時に、翌年以降の受験生が不健全な学びを強いられることがない素敵な問題も多く生まれました。これはたいへんよいことだと思います。
――不健全な学びを強いられることがない素敵な問題とは?
川島 対策を練らなければならない複雑な特徴のある問題ではなく、解き方を考えることや工夫することにフォーカスして、純粋に算数のおもしろさを味わえる問題です。今年の良問大賞では、今後の受験生に負担にならないという視点も加えて選びました。

「秀逸でオシャレな問題」も
――特に秀逸だと思われた問題は?
川島 トレンディ賞に輝いた灘中学校の1日目大問6は、もっともオシャレでした。例年、その年の西暦の数字をテーマにした問題は、一定数の学校で出題されています。今年は2025年ということで、2025に関する問題が出されました。

――どこがオシャレだったのですか?
川島 実は、受験生でなくても、小学生なら必ず目にしたことのあるものを、たいへんおもしろく応用しているところです。
――小学生が必ず目にしたことがあるもの?
川島 「かけ算九九」の表です。表を使って、45×45=2025になるということをおもしろく応用した問題でした。
1の段を1から9まで足すと45になります。2の段の合計はその2倍になり…というのを9の段まで繰り返して全部足すと、2025になります。この理屈が頭の中にストンと落とし込まれていて、それを応用できるかどうかが絶妙に問われているのです。
――なるほど!
川島 問題の中では、例として(6+7+8)×7+(6+7+8)×8=315が挙げられています。つまり、(連続するいくつかの数の合計)×(連続するいくつかの数の合計)=315となる組み合わせの数を探していくことになります。315を素因数分解すると3×3×5×7なので、ここまでわかれば煩雑な計算を避けられます。
――素因数分解は、小学校の算数では「約分」として学んでいますね。確かに、これなら算数で学んだことをベースにして考えれば、答えにたどり着けそうです。
川島 出題もそうですが、素晴らしい採点方式を採用している学校も増えてきました。そうした出題も含めて、今年の良問を見ていきましょう。
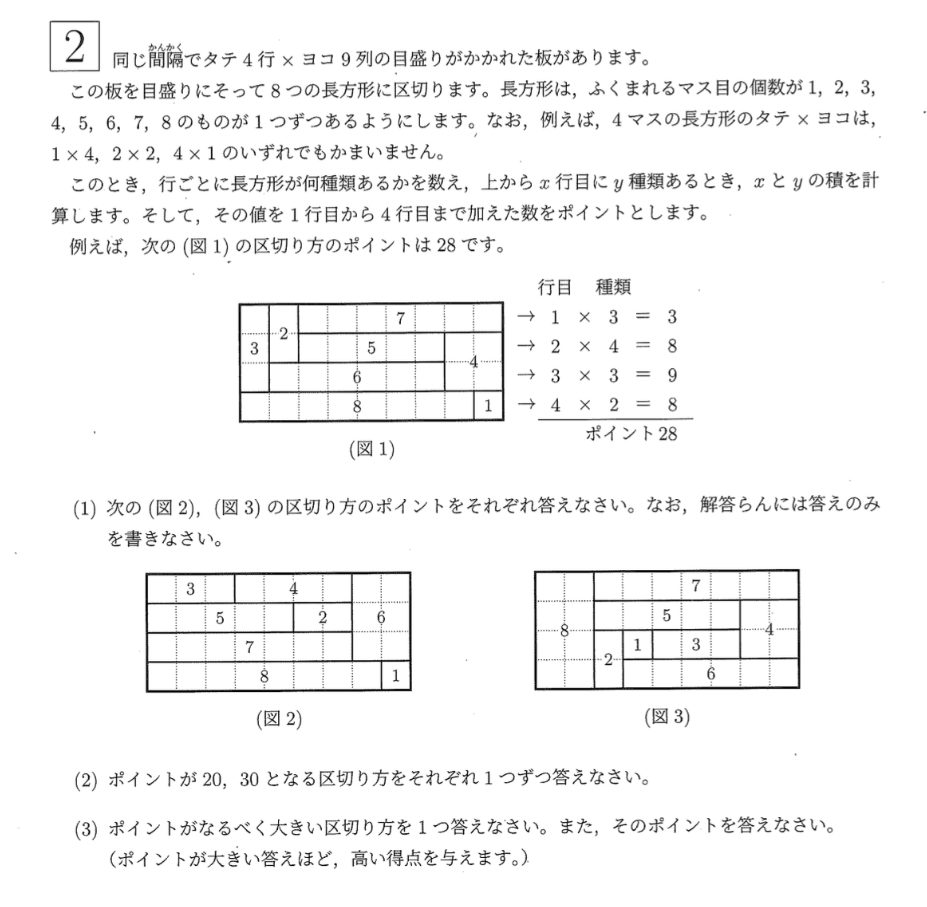
【グランプリ】開成中学校 大問2
――グランプリに輝いた理由は?
川島 事前知識があるかどうかで解答時間に差がつきにくい点が優れています。つまり、このことに気がつけば解けるという、いわゆる「解き筋」がない問題なのです。といって、ダラダラ適当に解いてもいけないわけで、自分なりに考えて工夫しなければなりません。
――採点方式は〇×ではないですね。
川島 「ポイントが大きい答えほど、高い得点を与える」という採点方式も秀逸だなと思います。時間内にあれこれ考えることを推奨した問題だと言えるでしょう。
――ぱっと見、図形パズルやゲームのようです。解けたら「やった!」と快感を味わえそうです。
川島 こういう出題が他の学校でも続いたら、詰め込み勉強の負担が減っていくと思います。そういう意味でも、良問です。
【ベスト誘導賞】普連土学園中学校 1日午前4科大問6

――問題文が会話形式ですね。
川島 会話形式が優れた誘導になってます。誘導に従うことによって、論理的に思考を発展させられます。
――その他の特徴は?
川島 問題に対して、複数の解き方を提示しているところも素晴らしいと思います。ひとつの問題をさまざまな解き方で味わうことは、算数や数学の醍醐味であり、算数や数学好きの人はよくやっていることです。
この問題でも、適切な誘導によって、受験生は複数の解き方があることを理解し、算数のおもしろさにたどり着けるでしょう。
――受験においては、とにかく正解できればそれでよいのでは?
川島 受験生にしてみたら、複数の解き方を学ぶことは、遠回りしているように感じるかもしれません。しかし、「いろんな解き方を試して、算数の醍醐味をぜひ味わってください」という出題者からのメッセージが込められている素晴らしい問題だと思います。
【ベスト体積賞】フェリス女学院中学校 大問3

――この問題の特徴とは?
川島 これは、どこを軸に回転するかで、ドーナツになったり円柱になったり、さまざまな形に変わる立体の問題です。体積を求めるのに必要な3.14をかける計算をまとめる前提で問われており、計算負荷を減らす形式になっているのが特徴的です。
――問題に込められているメッセージとは?
川島 その都度計算するのではなく、「計算をまとめる工夫をすることを学び、それを身につけてきてください」というメッセージがあると思います。
実際、受験勉強を通して計算の工夫する習慣を身につけたり、さらにそこに楽しみを見出したりできると、その先の数学でもつまずきにくくなりますから。
算数の楽しさを味わいながら学んでほしい

――今年の受験生にメッセージをお願いします。
川島 結果が良かった人もいれば、そうでない人もいるでしょう。いずれにせよ、中学受験という舞台に上がり、努力を重ねて挑戦したこと自体、すごいことだと思います。偉業です。みなさんにとって、縁があった学校が良い学校であり、良い学校であってほしいと願っています。
――これからの受験生、受験を考えている子どもや親御さんへのアドバイスは?
川島 日本の中学受験の算数問題は、考えることの楽しさ、工夫する喜びなどを感じられる問題が多く、世界に誇れる立派な文化だと思います。
入試問題は、学校からのラブレターです。学校側は真剣に作っているし、おもしろい問題を出しています。ぜひ、算数の楽しさを味わって学んでほしいと願っています。
――じっくり考えられる子にするには?
川島 小さいときからあえて学ぼうと意識せず、本人が夢中になっていることが、のちのちじっくりものを考える上で役に立つと思います。たとえば電車が大好きな子、積み木遊びに夢中になっている子は、それぞれ楽しみながら自然にいろいろなことを吸収し、学んでいます。そういう学びを邪魔しないことが大切だと思います。
――ありがとうございました。
* * *
ワンダーファイの良問大賞のページでは、他にも多くの入賞問題が紹介されています。各問題の狙いから、それぞれの学校の教育方針、生徒に期待する資質なども読み取れます。お子さんの志望校選びや入試の傾向分析に活用してください。
こちらの記事もおすすめ

お話を伺ったのは

取材・文/ひだいますみ





