算数は得意ですか？ 子どもが「宿題を見て」だとか「教えて」と頼ってきた時、できれば分かりやすく対応してあげたいですよね。例えば「ひし形」は小学校の4年生になると習います。「ひし形をどうやって描くのか、分からなかったから練習したい」とわが子が言ってきたら、どうしたらいいのでしょうか？
そこで今回は、ひし形の上手な書き方をまとめてみました。パパ・ママの教養として、来年度わが子が4年生に上がるという家では、ぜひ学び直してみてくださいね。
ひし形とは？
この記事では、ひし形の上手な書き方を学びますが、そもそもひし形とは何なのでしょうか？ 普通の四角形や平行四辺形とは何が違うのでしょう？
ひし形の定義
ひし形とは、辞書にはどのように書かれているのでしょうか。あまりにも基本的な言葉なので、「ひし形とは何だろう？」と辞書を引く機会は、なかなかないと思います。小学館の辞書『大辞泉』を調べると、以下のように書かれています。
＜１ ヒシの実のようなかたち。
２ 四角形のすべての辺の長さが等しいもの。このうち、すべての角が直角のものは正方形。斜方形。りょうけい。＞（小学館『大辞泉』より引用）
1番のヒシの実とは、池や沼、川に自生する水草の実で、鋭い突起を持った形をしています。ヒシは葉っぱのほうがまさにひし形なので、ヒシの実というよりも葉のような形という説明でもいいのかもしれませんね。
ひし形の特徴は、四角形の全ての辺（線）が同じ長さだとされています。そうなると、「正方形なんじゃないの？」と思うかもしれませんが、辺と辺の触れる角の角度が直角ではない（辺の長さの同じ）四角形を、ひし形というのですね。
四角形とは違う!? 四辺形の定義
では、似たような言葉で四辺形という言葉があります。四「角」形ではなく四「辺」形。違いは何なのでしょうか？ 辞書で調べると、
＜四つの辺からなる多角形。四角形。＞（小学館『大辞泉』より引用）
とあります。四「角」形とはあくまでも角の数に注目した言葉で、同じ図でも辺（線）の数に注目した言い方を四「辺」形というのですね。
四辺形と四角形は、辺（線）と角のどちらに注目したかの違いであって、図形そのものは4つの角と4つの辺（線）を持つ同じ図形を意味します。
平行四辺形の定義
では、四辺形の中でも、よく耳にする平行四辺形とは何でしょうか？ 四辺形は辺（線）の数に注目した図のとらえ方でした。この4本の辺のうち、向かい合う辺同士が平行の図形を、平行四辺形と言います。
＜二組みの向かい合う辺が、それぞれ平行である四辺形。＞（小学館『大辞泉』より引用）
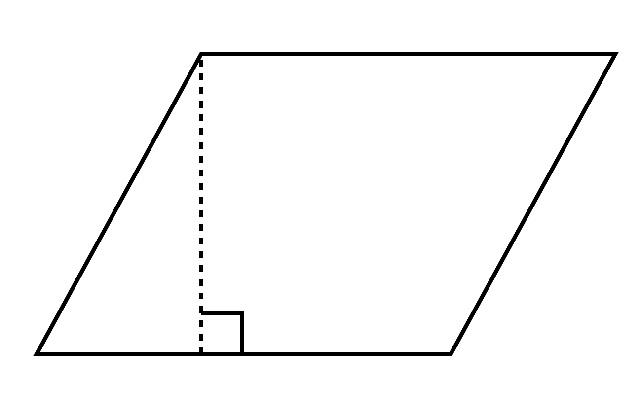
ちなみに英語ではparallelogramと言います。「parallel」（パラレル、並行の）といった言葉が見られますね。ひし形も向かい合う2組の辺が並行に並ぶので、平行四辺形の一種とも言えます。
ひし形の書き方
ひし形の定義、四角形の定義、四辺形の定義などを整理してきました。角だとか、辺だとか、直角だとか、文系の人生を歩んできたパパ・ママたちからすれば、懐かしい響きの言葉ばかりではないでしょうか？
ひし形は、同じ長さの辺が直角ではない状態で連続した四角形でした。辺と辺の触れ合う角の角度が、直角の場合は正方形と言います。正方形であれば簡単に書けそうですが、ひし形はどうやって作図すればいいのでしょうか？
コンパスを使って作図する
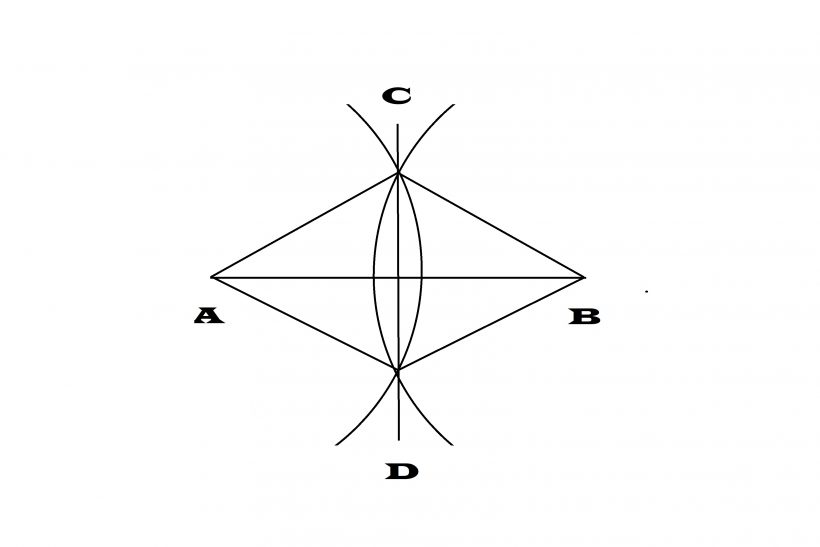
最もオーソドックスな作図の方法は、コンパスを使います。「コンパスなんて小学校に通っていた時代以来、使っていない」という人がほとんどだと思います。あのコンパスが手元にあれば、簡単にひし形は作図できます。子どもが学校で使っているコンパスを借りて、以下のような手順で作図を練習してみてください。
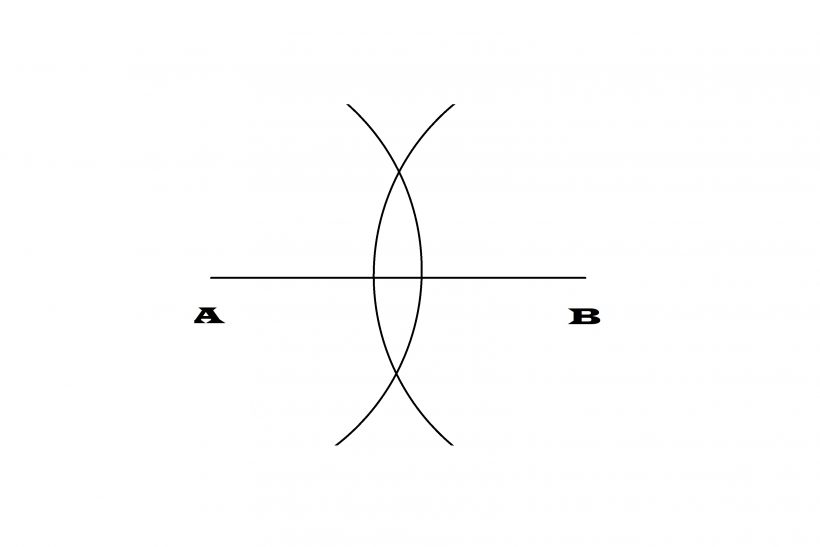
（1）線分ABを引く。
（2）点A、点Bからそれぞれ、向かい合った点の方向に向かって同じ半径の半円を描く。
（3）円と円が重なる点（CとD）同士に線分を引く。
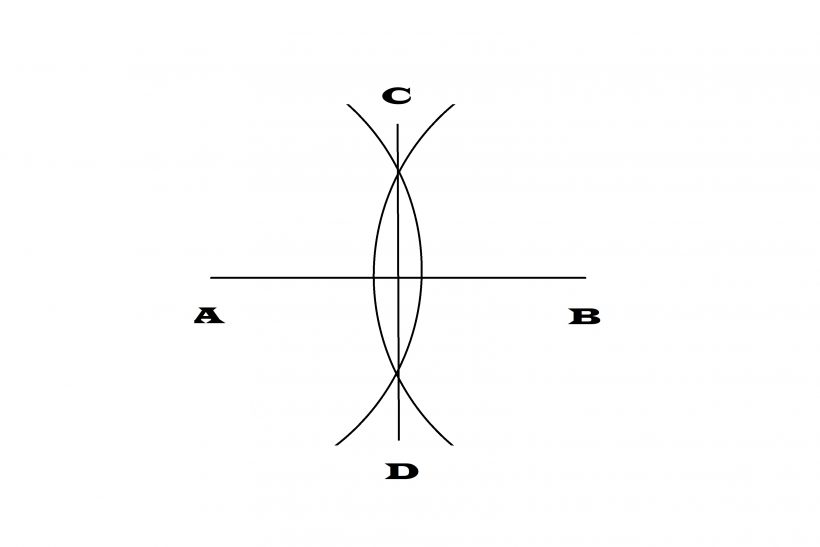（4）ABCD、4つの点を線分で結ぶ。
分度器を使って作図する
コンパスが手元になかったらどうしたらよいでしょうか。
その場合は、わが子に分度器を持っているか聞きましょう。文系の人生を歩んできたパパ・ママには、分度器も懐かしい存在ではないでしょうか？ 分度器と定規があれば、ひし形が作図できます。
その場合、ひし形の特徴「全ての辺（線）の長さが同じ」を思い出すと分かりやすいです。
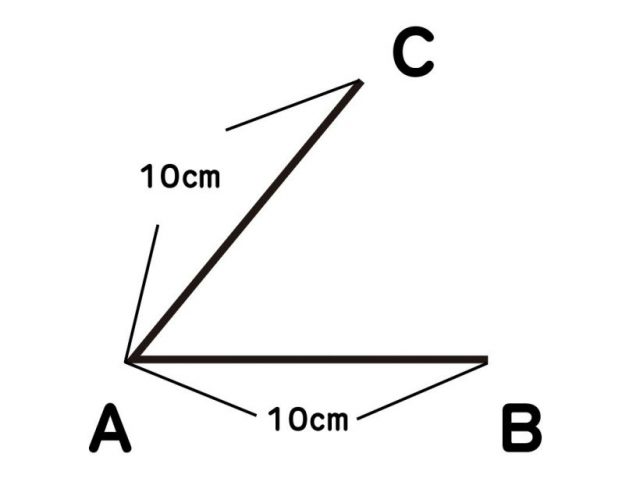
（1）線分ABを一定の長さで引く（ここでは10cm）。
（2）点Aから適当な角度（例えば50度）を決めて、その角度に向かって、線分ABと同じ長さの線分AC（10cm）を引く。
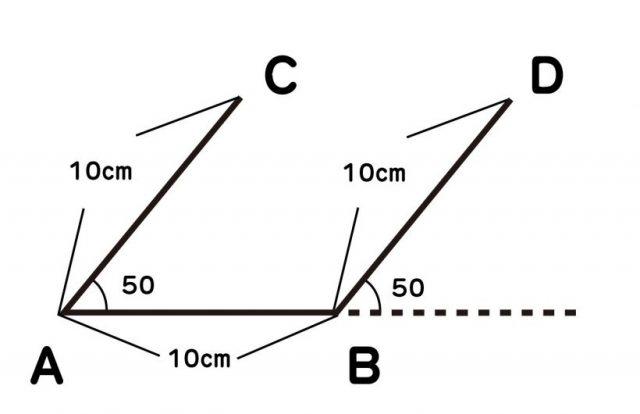
（3）線分ABの点Bに分度器を合わせ、点Aと同じ角度（この場合は50度）の線を引き、線分AB、線分ACと同じ長さの線分BDを描く。
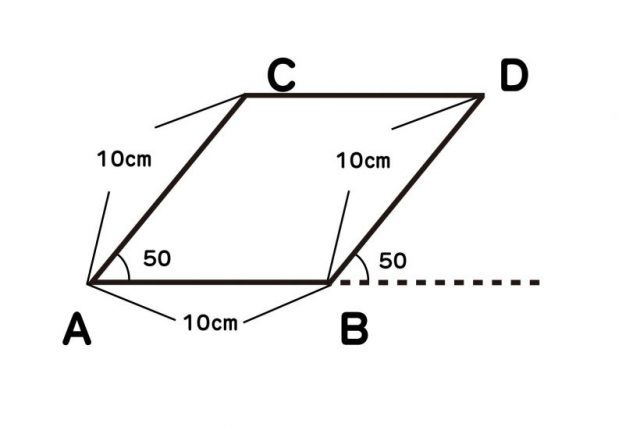
（4）点Cと点Dを線分で結ぶ。
定規だけで作図する
仮に子どもがコンパスも分度器も学校に忘れてきたとしたら、どうやってひし形を作図すればいいのでしょうか？ 自由度が多少制限されますが、定規1本でも作図は可能です。その場合は、作図の前に垂直二等分線について思い出しておきたいです。
垂直二等分線とは？
垂直二等分線とは、辞書を引くと以下のように解説があります。
＜ある線分の中点を通り、その線分に垂直な直線＞（小学館『大辞泉』より引用）
分かりやすく言えば、「＋」のように2本の線分が垂直に交わり、交わった点でそれぞれの線分がきれいに2つに分かれている状態を、垂直二等分線というのですね。
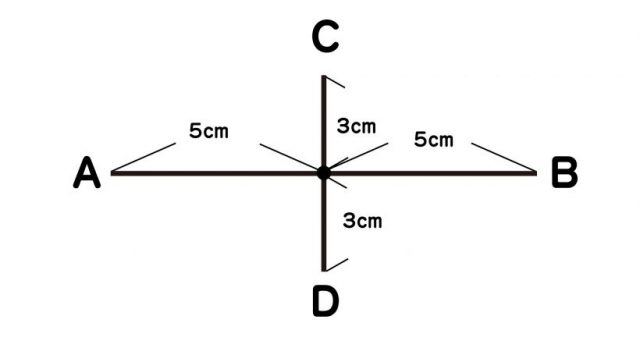
今回のテーマであるひし形に注目すると、ひし形にある4つの角を、向かい合った角同士で線分で結べば（対角線）、必ず垂直二等分線が出来ます。逆の見方をすれば、先に垂直二等分線を引いて、各線分の両端を新たに線分で結べば、ひし形ができるということになります。
（1）例えば10cmなど、中心が分かりやすい線分ABを引く。
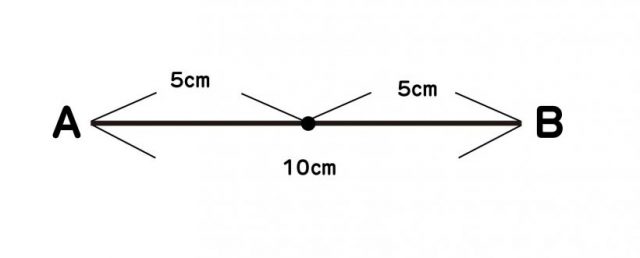
（2）中心である5cmの点に、CからDに向かって、たとえば6cmの線分CDを直角に引きます。その際、CとDから3cmずつの点が、線分ABの5cmの点に交わるように線分を引きます。
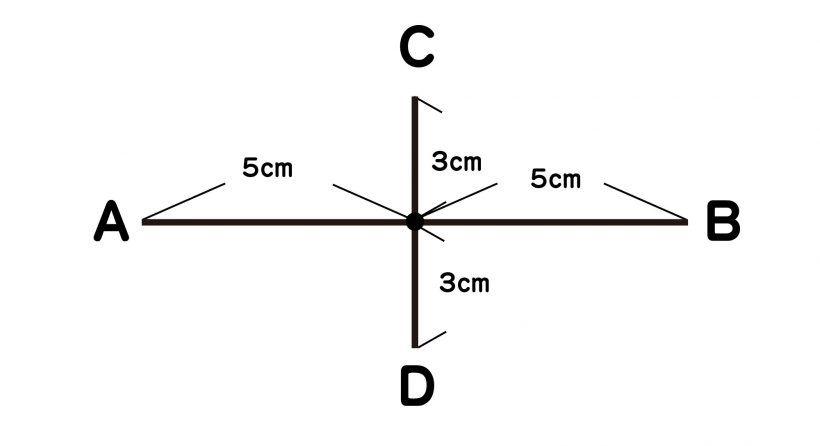
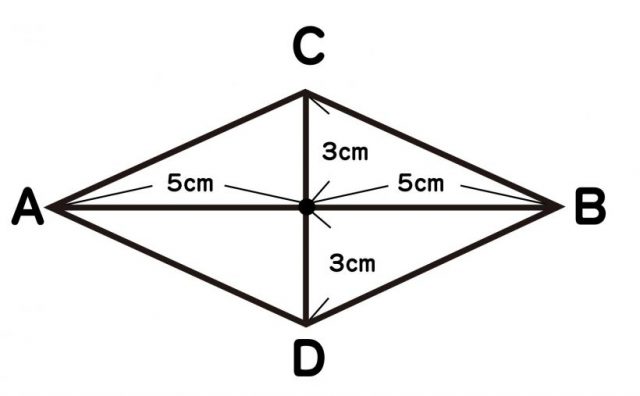
（3）「＋」のような垂直二等分線ができたら、各線分の両端、ABCDを定規で結べば、ひし形の出来上がりです。
宿題の手伝いで大人の「脳トレ」にしてみては？
子どもが宿題を「教えて」と頼ってきた時、子どもの学年が上がるほどに「分からない……」という瞬間が増えてくると思います。さらに毎日の忙しさが重なると、思わず「熟の先生に聞いて」「学校の先生にもう1回聞いて」と、投げ出してしまうかもしれません。
しかし、子どもから寄せられる質問は、子どもと一緒に賢くなるチャンスでもあります。大人の「脳トレ」だと思って、インターネット上で一緒に調べ、正しいやり方を一緒に考え出してあげると、大人の学び直しにもなりますし、子どもの頭にも入りやすいはずです。何より、親子でコミュニケーションをとるきっかけにもなりますね。
「ひし形の書き方を教えて」と子どもに頼られたら、このページを繰り返し、参考にして、上手に導いてあげてくださいね。
文／坂本正敬
