素因数分解とは何か
素因数分解とは、正の整数(自然数)を、素数のかけ算(積)で表すことです。まずはここに出てきたそれぞれの言葉の意味をチェックしましょう。
正の整数(自然数)は「1」「2」「3」「4」「5」などの数字です。同じ数字でも小数・分数・マイナスの数は正の整数には含まれません。また「0」も中学生・高校生で学ぶ数学では、正の整数に含まずに考えます。
素数とは「1」と「その数字」以外では割れない数のことです。素数の例として「2」「3」「5」などが挙げられます。
素因数分解のコツは素数の暗記
スムーズに素因数分解の問題を解くには、素数の暗記がポイントです。素数を覚えていなければ、まずはその数が素数なのかを確認しなければならず、問題を解くのに手間がかかります。
まずは「2」「3」「5」「7」「11」「13」「17」「19」くらいまでの素数を暗記しておくと解きやすくなるでしょう。

素数の当たりをつけるときのコツ
素因数分解の問題を解くときには、正の整数を割り切れる素数は何かを素早く見つけることが重要です。そのためには、割り切れる素数を確認する方法も暗記しておくとよいでしょう。
正の整数が2の倍数であれば一の位は「0」「2」「4」「6」「8」のいずれかになることや、4の倍数であれば下2桁が4の倍数になることを知っていると、どの素数で割り切れるのか当たりをつけやすくなります。
ある数を2乗した数である平方数も、よく登場するものは覚えておくとスムーズに計算可能です。例えば11の平方数「121」や、12の平方数「144」、13の平方数「169」を覚えておくとよいでしょう。
また小さな素数から割っていくのも素早く解くコツです。
素因数分解のやり方
ここでは実際に素因数分解を解いていきましょう。
やり方を見ていくのは「20」の素因数分解です。「20=2×10=2×2×5=2²×5」となりますが、これを筆算で解くやり方を見ていきましょう。
素因数分解する数を素数で割る

まずは、「20」をいちばん小さな素数「2」で割れるか試してみましょう。「20」は「2」で割れます。1の位が「0」であることからも「2」で割り切れる数だと分かります。

筆算で表すときには、まず「20」の左側に曲線を引き、その左側に「2」を、「20」の下に横線を引き、その下に「10」を書きましょう。
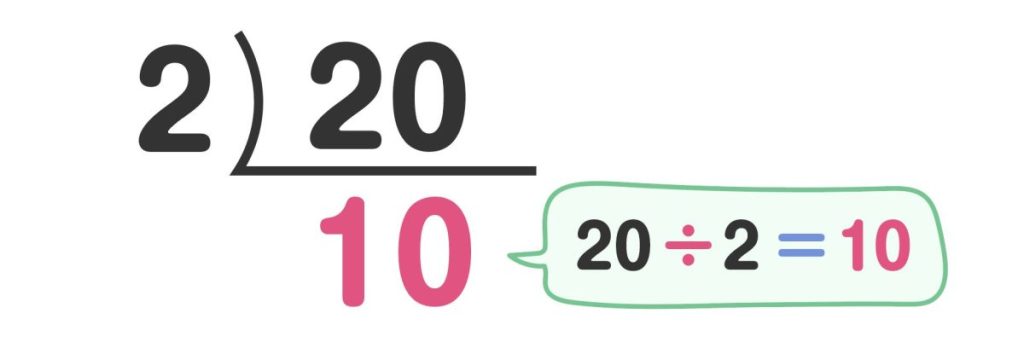
これで「20=2×10」まで計算できました。
割った答えが素数になるまで割り算を繰り返す
次は、上で出した割り算の答え「10」に注目して、こんどは「10」を割れる素数を見つけましょう。小さな素数から試していくと「2」で割り切れると分かります。
「10」の左側に曲線を引き、その左側に「2」を、「10」の下に横線を引き、その下に「5」を書きます。

これで「20=2×10=2×2×5」まで計算できました。
左の数と下の数をかけ算で書く
筆算をしたときに、曲線の左側にある数と、いちばん下に書いた数をかけ算で書きます。この問題では「2×2×5」です。
「2×2」は「2²」と表せるため、回答は「2²×5」となります。

練習問題を解いてみよう

素因数分解をすらすら解けるようになるには、練習が必要です。上でやった「20」の素因数分解の手順を参考にして、練習問題を3題解いていきましょう。
問題1)14を素因数分解しましょう
「14」を素因数分解するときにも、まずどの素数で割れるかを考えます。小さな素数から試していくと「2」で割れると分かるでしょう。1の位が「4」であることからも「2」で間違いありません。

「14÷2=7」のため、筆算では「14」の左側に「2」を、下に「7」を書きます。「7」は素数のため、ここで計算は終了です。
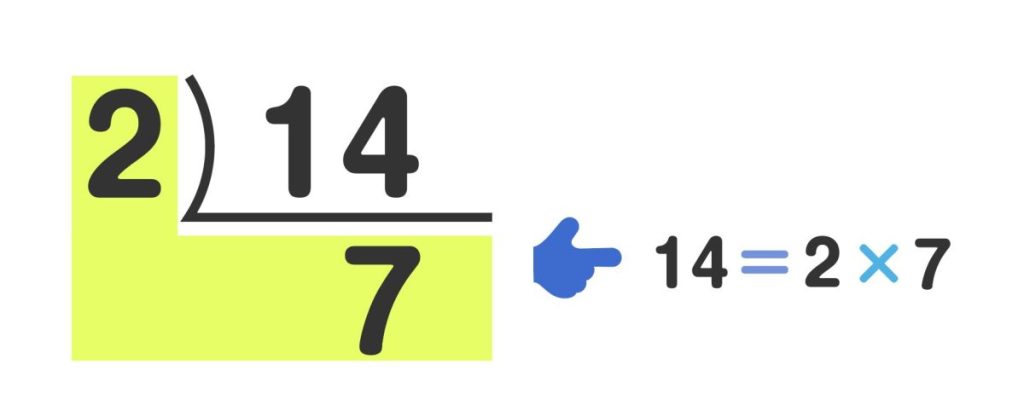
「14」の左側といちばん下の数字をかけ算にした「14=2×7」と求められます。
問題2)36を素因数分解しましょう
「36」の素因数分解でも考え方は同じです。まずは「36」がどの素数で割れるかを探します。「2」で割れるため「36」の左側に「2」、下に「18」と書きましょう。

次は上で出た数字の「18」に注目します。「18」を割れる最小の素数は「2」で、下に書く数は「9」、「9」を割れる素数は「3」で下に書く数は「3」です。
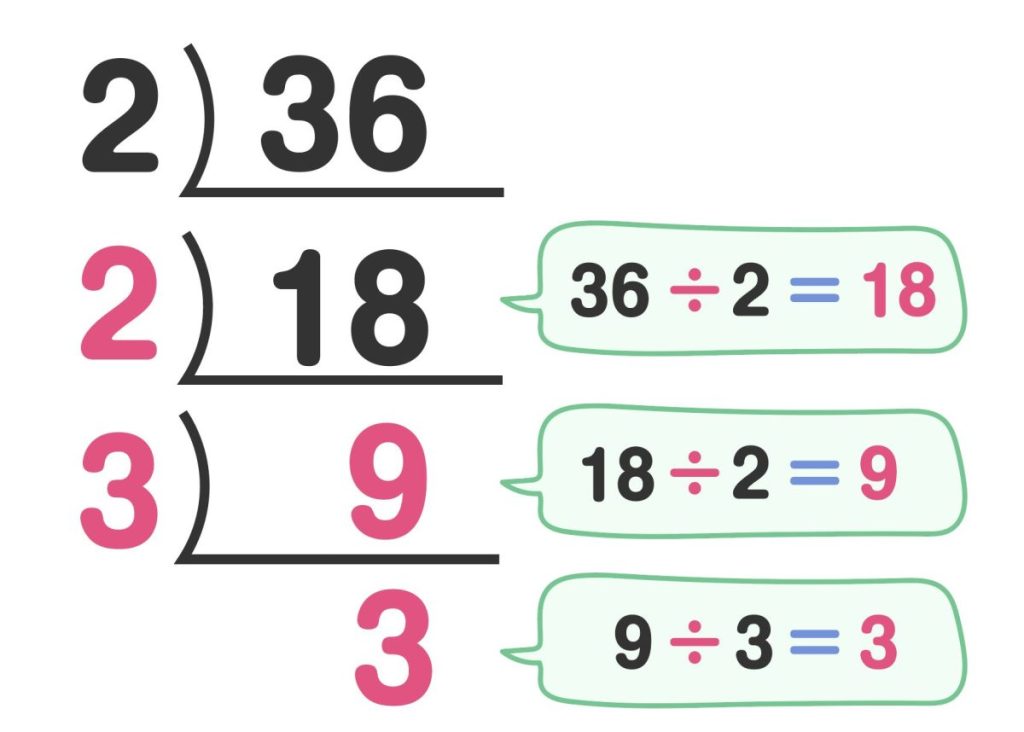

計算式で表すと「36=2×18=2×2×9=2×2×3×3=2²×3²」となり、答えは「2²×3²」です。
問題3)148を素因数分解しましょう
数字がどれだけ大きくなってもやることは変わりません。「148」は素数「2」で割れるため、左側に「2」を、下に「74」を書きます。

「74」も「2」で割れるため、左側に「2」を、下に「37」を書きましょう。「37」は素数のため、ここで計算は終了です。


計算式は「148=2×74=2×2×37=2²×37」となり、答えは「2²×37」となります。
素因数分解はコツが分かればスムーズ

素因数分解をスムーズに解くには、コツを押さえておくことが重要です。よく使う素数を暗記し、正の整数を割る素数の当たりをつける方法を知っていれば、比較的簡単に答えを求められます。
数字が大きくなっても必要なポイントは変わりません。どんどん練習問題にチャレンジして慣れていけば、すらすら解けるようになります。
こちらの記事もおすすめ
構成・文/HugKum編集部






