目次
日常生活の中で「イメージ力」=「算数感覚」を育てておきましょう

5+3=8という計算はできるのに、「おじいさんから5個、おばあさんから3個のみかんをもらいました。全部でみかんは何個になったでしょう?」という文章問題がすぐに解けない1年生がいます。
5個のみかんや3個のみかんを頭の中に思い浮かべ、それを5や3という数字に結びつけて考えるイメージ力が足りないと、計算式の真の意味は理解できません。イメージ力とは、数や計算式を実際のモノや状況に結びつけて、具体的に思い浮かべる「算数感覚」です。
算数感覚を高めることで、計算の仕組みが理解できるようになり、応用力も高まります。計算ドリルを数多くこなしても、文章問題を解くためのイメージ力は高まりません。くり上がりの足し算や、くり下がりの引き算の数の仕組みを理解するためにも、積み木やブロックなどの玩具やスプーンやフォークといった日用品など、実際にモノを動かして数を数えたり、絵を描いてそれを数えたりするなどして、算数感覚を育むことが望ましいでしょう。
指を使って数を数えることを否定しないでいい
指は、最も身近で便利な、数を数えるための道具です。いつでもどこでも、すぐに使えるため、古来より民族を超えて、広く使われてきました。幼児期において指を使って数えることは、数というものを視覚的に理解するために欠かせない行為となります。片方の手では5までの数を数えることができるうえ、5本の指でひとつの手となり「5のまとまり」を意識できます。両手を使えば10まで数えられ、「10のまとまり」が「5のまとまり」2つ分だと言うことも視覚的に認識できます。
算数を学び始めた一年生の時期には、多くの子どもが指を使って数を数えたり、計算をしようとしたりしますが、それをやめさせる必要はありません。かつては指を使って計算することは、いけないことのように言われていましたが、最近では数という抽象的な概念の理解を視覚的にサポートすることになると考えられています。
指を折れば10まで数えられ、次に指を開くと20まで数えられます。一桁の足し算なら、10を超える時点で、繰り上がりを意識することもできます。また、一年生で習う「さくらんぼ計算」で必要となる10の数を作る際も、指を使うと視覚的に答えが導けます。指を使って数える、計算することは、数の概念を理解するのに必要なことだと覚えておきましょう。
「一対一対応」を知ることが、数の多少を判断する際の要に
コップひとつにストローが1本といった「一対一対応」は、数の多少を判断する際に必要です。例えば、皿とケーキがあったとします。皿1枚にケーキが1個と、順々に皿にケーキを載せていき、どちらも余ることがなければ皿とケーキはが同数であり、どちらかが余れば、余った方が多いということがわかります。
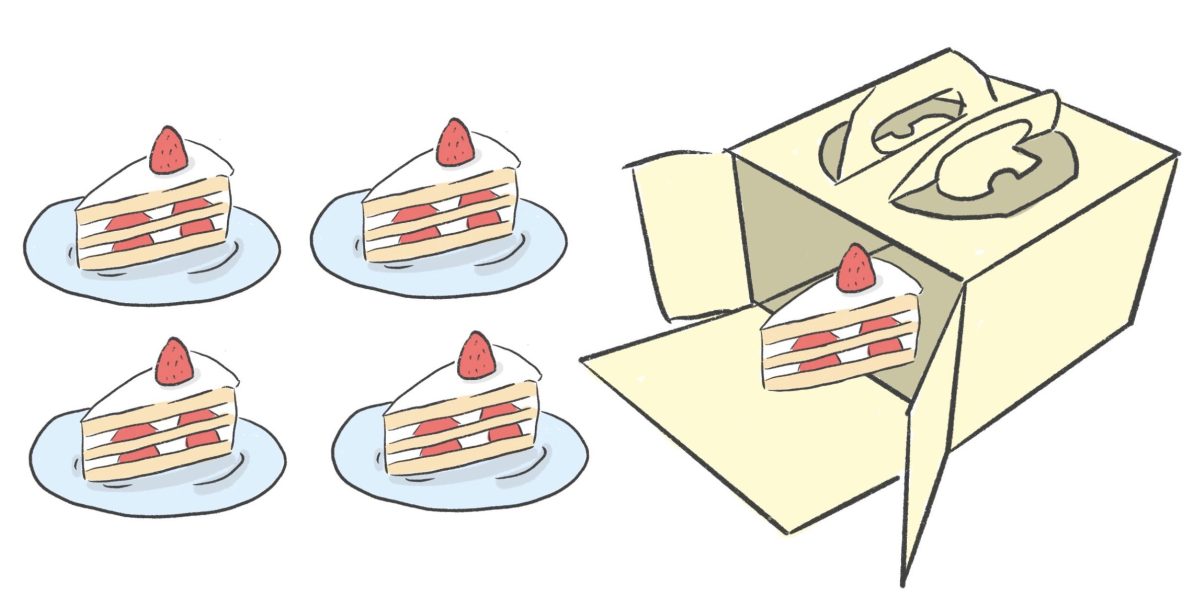
「一対一対応」は、数の概念の理解、そして計算の基礎を築くうえで不可欠で、幼児期に具体物を使った一対一対応の経験を積んでいると、小学校に入ってからの算数の学習が理解しやすくなります。
数えたいモノをひとつずつ指さしして、「1,2,3…」と数を当てはめて数えることも、1対1対応をしていることになります。「1,2,3…」と100までの数唱ができれば、指でひとつずつ指差しながら数えることで、理論の上では100までの数は数えられることになります。
卵パックを使って「10のまとまり」を理解する
しかし、「一対一対応」で100まで数えるのは、途中で間違いが起きたりもしてなかなか難儀です。そうした際に活用できるのが、「10のまとまり」を意識しながら数える方法です。おはじきを10個数えたら、「10のまとまり」としてひとつにまとめます。「10のまとまり」がいくつできたかで、全体の個数を導き出せるのです。
「10のまとまり」ができると位が1つ増える。この、十進法の考え方がわかっていないと、くり上がり・くり下がりの計算が苦手になる原因になります。10個入りの卵パックを使って「10のまとまり」を視覚的に理解しやすくしておきましょう。
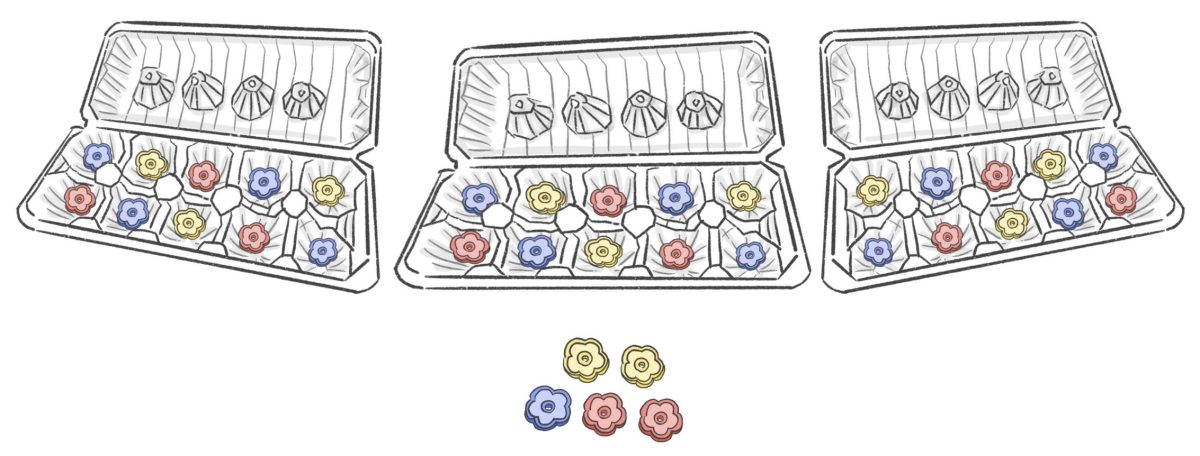
例えば、35という数字の成り立ちを理解するために、35個のおはじきと卵パックを使って数えてみましょう。卵パックの卵を入れるくぼみに、おはじきをひとつずつ入れていきます。おはじきで卵パックのくぼみが全部埋まれば、そこで10のまとまりができます。次の卵パックにもおはじきを入れていくと、おはじきで埋まった卵パック3つと、5個のおはじきになります。
これで、おはじき35個が「10のまとまり」3つと、5個のおはじきで成り立っていることがわかります。
量を示す「集合数」と順番を示す「順序数」。子どもにとって難しいのは…

数には、モノの量や個数を表す「集合数」と、順番や順序を表す「順序数」があります。子どもにとって、この順序数を理解することは、集合数を理解するより一般的に難しいと言われています。
子どもが一列に並んだときに、「前から4番目」の「〜から」という基準をどこに置くのか、一番前の子どもを1番目と数えるのか? 次の子を1番目と数えるのか?と、混乱することも珍しくありません。
また、「自分の前に3人、自分の後ろに5人が並んでいる場合、全部で何人?」と集合数を尋ねる問いでは、自分を数えるのを忘れて計算する子も少なくありません。これが「自分は前から4番目、自分の後ろに5人います、全部で何人?」と、順序数と集合数が文章の中に混在すると、ますます混乱してしまいます。
順序数を理解するための体験を
順序数を理解するには、数える対象の絵を描いて、その上に数字を振ると理解しやすくなります。また、普段の生活で、順序数を意識させるような言葉がけをすることも、理解を深めるために有効です。
例えば、積み木を並べて、「4番目の積み木はどれかな?」と尋ねたり、「上から2番目の引き出しから、フォークとスプーンを3本ずつ出して」と頼んだり、公園のブランコの順番で並ぶ際に、「あなたの前には何人いる? あなたは何番目?」と尋ねてみたりするとよいでしょう。遊びや生活の中で繰り返し「順序数」に触れる機会があると、徐々に理解ができるようになっていきます。
指や手を使ってつかむ「算数感覚」を大切に

「長さ」「量」「重さ」「面積」などの数字と単位を組み合わせた測定値は、実体験が伴わないと、それらが意味することの理解やイメージが、極めて難しくなります。
「長さ」「量」「重さ」「面積」は、実体験に勝るものなし。まずは、手を使って測ってみよう
「30㎝」「100ml」といった文字を目にしても、実際にそれらの長さや量を体験したことがなければ、どれくらいの長さなのか、量なのかは想像がつきません。こうした「長さ」「量」「重さ」「面積」に触れる機会を幼児期に増やしておくと、小学校の算数の授業でこれらを習う際に、より理解がしやすくなります。
小学校では、定規やはかり、計量カップなどを使って計測をしますが、幼児期ではまだ、そのような計測をする必要はありません。ひもの長さを自分の手のひら何個分というように、まず、自分の手を使って測ってみようという体験をしましょう。
何か任意で決めたものを基準にして長さや量を測る単位のことを、「任意単位」と言います。一方、定規やはかり、計量カップなどを使って測る、cm、ml、gなど、世界共通の単位は「普遍単位」と言います。
任意単位での測定は、測る人によって測定値が異なります。例えば、黒板に書かれた直線を、手のひらを使って測る場合、手の大きい子と小さい子では「手のひら○個分」の○に入る数字が変わってしまいます。また、コップと水筒を使って、2つの水筒の容量の違いを測ってみてください。同じコップで測らないと水筒の容量は比べられないことに気づきます。
実際に子どもが自ら体験し発見することで、「長さ」や「量」を実感し、イメージできるようになっていきます。重さや面積も同様で、はかりやメジャーなどで実際に測ってみることで、数字が示す数値をイメージできるようになります。
算数感覚を育てることで算数が好き!と感じられる子どもに

「算数が好きだ」と子どもが感じるようになるには、日常生活の中で、数や量を比べたり、重さを測ったり、順番を数えたりなどの実体験を増やすことが重要となります。実際に手に取ったり、指差しをしたり、体を使って測るなどの体験は、ドリルやタブレットを使って計算式を数多く解いたりするよりも、ずっと効果があります。ぜひ、小学校に入るまでの準備として、ご家庭でさまざまな体験をさせてあげてください。
「算数感覚」について、こちらの記事も合わせてお読みください

取材・構成/仲尾匡代

山本良和先生





