目次
速さは単位が理解できたもの勝ち!
速さの問題で一番重要なのは「単位の理解」です。
速さの計算が当てずっぽうになってしまう多くの子どもたちは、秒速や分速、時速といった単位がしっかり理解できていないからです。小学校低学年でmやkmなどの長さの単位を学びますが、分速mや時速kmといった速さの単位が出てくると途端に特別なものと感じてしまい、難しく捉えてしまいます。
しかし、たとえば分速は「1分間に進む道のり」を表しているだけ。速さの単位も本質的には長さの単位でもあることを理解できれば、特別な概念ではなくなるはずです。
公式の暗記ではなく本質的な理解を
「時速72kmは秒速何m?」という問題に対して、「時速km÷3.6=秒速m」という公式を使って解くこともできます。
速さの単位に限らず、単位の本質的な理解のためには、むやみに公式を覚えることはおすすめしません。それよりも時速72kmは「1時間(=3600秒)あたり72km進むという意味だから、まず72kmを72,000mに変換しよう。そして、これを1秒あたりにするためには、3600秒で割る必要がある」というプロセスをしっかりと踏んで理解することのほうが長い目でみたときに応用が利きます。
ご家庭でも、
「分速20mで10分進んだらどれだけ進む?」
などとお子さんに質問し、基本的な単位の意味をしっかり理解させてください。
電車が好きなお子さんは、新幹線を例にとるとよいですね。
「今日はのぞみに乗って東京から新大阪まで行くよ。どれくらいの距離を進むかな? のぞみの速さは時速210kmで、新幹線に乗っている時間は2.5時間だよ」
などと問いかけてみてください。
覚えるのは「速さ×時間=道のり」だけ
速さの公式は、「速さ×時間=道のり」だけで十分です。これさえ覚えておけば、あとは分からない部分を□に置いて逆算すれば問題なく解けます。「3つの公式を覚えましょう」と言われることもありますが、実際にはかけ算の公式を一つ覚えるだけで、あとは逆算を使えばすべての問題が解けます。
そして慣れてくればいちいち□におくことなく、3つの公式を自然に使えるようになります。
「速さ」でつまずきやすいのはココ!
×「速さ×時間=道のり」があやふや

この問題では、毎時60kmは速さ、道のりが12kmです。基本の「速さ×時間=道のり」がしっかり身についていれば、時間を求めるためには「道のり÷速さ」を計算すればよいとわかります。
×数字を適当に計算してしまう

ここでは、歩くのにかかった時間(20分)と自転車でかかる時間(9分)をたしてしまっています。秒速1.5mの速さで20分歩いた道のりが、家から図書館までの道のりですよね。同じ道のりを進むのに、自転車だと9分かかるということが理解できれば、自転車の速さは、道のり÷時間で計算できることがわかります。
もう一つのポイントは、秒速1.5mに合わせて、20分を1200秒に直して計算することですね。
「速さ×時間=道のり」と単位の変換をしっかり理解して、速さの問題のつまずきをクリアしていきましょう。
割合は、「もとにする量は何か」がわかればクリア!
割合の最大のポイントは、「もとにする量が何か」をきちんと理解すること。これさえできれば、割合の問題はほぼ克服できたと言えるでしょう。
割合というのは「何かと比べる」という作業なので、「どちらをもとにするのか」が非常に重要です。
「お父さんの体重があなたの2倍だとしたら、どっちを基準にしているのかな?」
といった感じで、どちらを「もとにして」比べているのかを考える習慣をつけられたら最高ですね。この場合、あなたの体重が「もとにする量」になります。普段の会話でこうした割合の話を取り入れることで、自然に割合の感覚が身につきます。
割合の概念は、子どもにとっては非常に抽象的なものなのです。そのため、すぐに身につくものではありませんが、一旦わかってしまえば、間違えることもなくなります。焦らずじっくりと付き合ってあげてください。
「の」があったらかけ算、に頼らないで
割合の問題の文章中に「の」があったらかけ算という「裏技」みたいなものがあります。
たとえば、「150円の4割は何円ですか」であれば、「150×0.4=60(円)」となるわけです。しかし、それに頼りすぎると、問題の順番や言い方が少し変わったときに混乱してしまうことがあります。そうした状況にならないように、割合の感覚をしっかりと理解し、自然に身につけることが大切です。テクニックだけに頼らず、根本的な理解を深めることが重要です。
「もとにする量 × 割合 = 比べる量」だけでOK!
割合の問題を解くには、「もとにする量 × 割合 = 比べる量 」の公式を一つ覚えればOK。速さと同じで、公式を一つ覚えるだけで、あとは逆算を使えばすべての問題が解けます。ただし、5割は0.5、20%は0.2というように、何割や何%を小数や整数に直す練習は必要です。この基本的な変換ができれば、ほぼすべての割合の問題に対応できるようになります。
割合でつまずきやすいのはココ!

「5割」の5の数をそのまま計算式に使ってしまっています。何割を小数や整数に直す練習をすれば、このつまずきはクリアできます。

もとにするのは□ページの方です。どちらをもとにするのか、そこを理解して割合の感覚をしっかり身につけることが大切です。
小数の計算は、小数点をそろえるだけでいい
小数の問題でつまずく理由は、小数点の扱い方を理解していないか、基礎的な計算力が不十分かのどちらかです。その見極めをしっかり行うことが鍵になります。
小数点の扱い方を理解していないのであれば、たし算やひき算では小数点を揃える、かけ算やわり算では小数点を正しく移動させる練習が重要です。
計算自体が苦手なのであれば、まずは計算ドリルなどを使って基礎をしっかり固める必要があります。
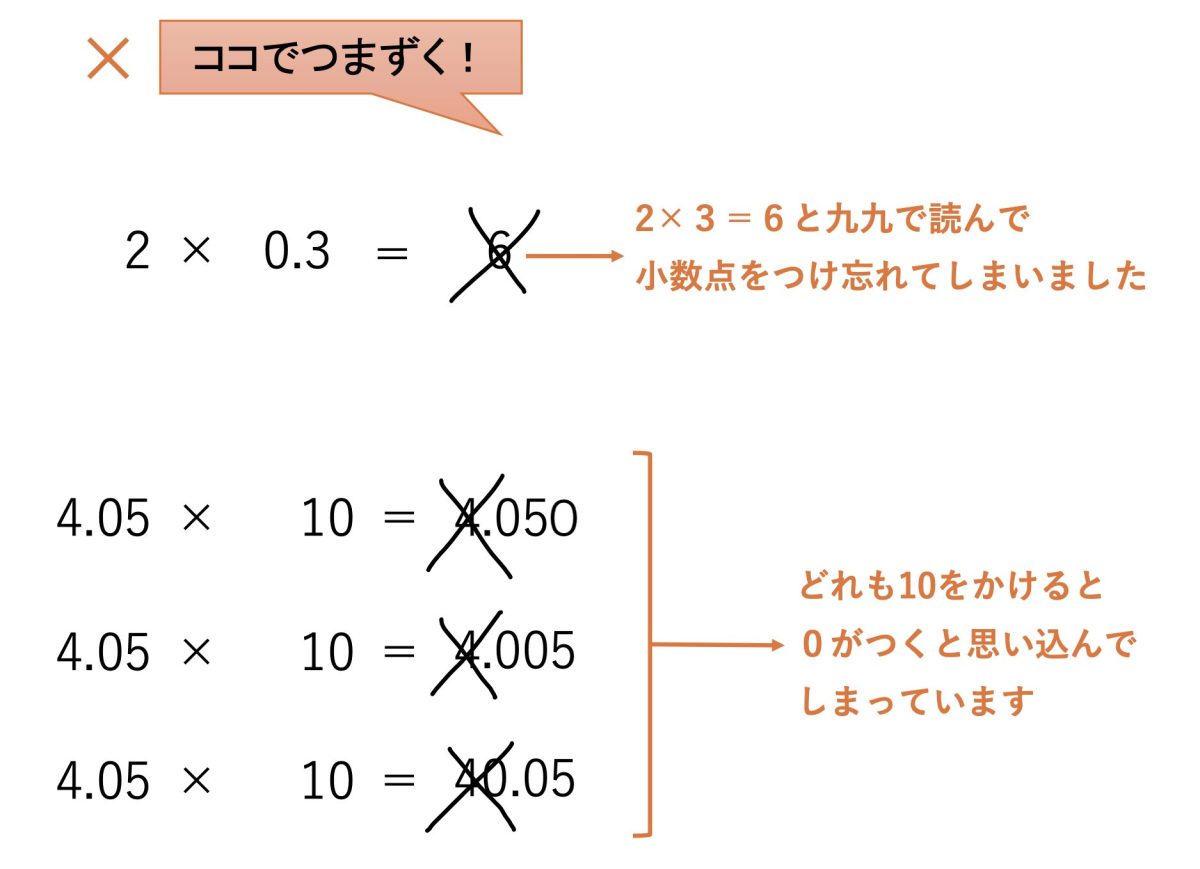
小数でつまずきやすいのはココ!
⚫︎小数点のつけ忘れ&ゼロをつければいいと勘違い
分数は通分と約分につきる
かけ算と九九は大丈夫?
分数は通分と約分ができるかどうかがポイントになります。どちらも、2年生で習った九九が威力を発揮するのです。
通分で、「6」と「8」の最小公倍数を見つけるとき、感覚的に「24だよね」とすぐに答えが浮かぶのは、かけ算の計算力がしっかり身についているからこそ。この計算力が自然に使えるようになると、最小公倍数を見つけることがスムーズにできます。通分が苦手な子どもたちの多くは、やはりこのかけ算や九九の力がまだ不足していることが原因である可能性が高いです。
さらに、約分の場面でも差が出ます。「36/48」を2で割ってしまうか、すぐに12で割れると気づけるかどうか。この差は、実際の計算スピードや正確さに大きく影響します。計算の効率や精度が上がることで、他の問題にも余裕を持って取り組めるようになり、これが長期的に見ても大きな違いとなるのです。
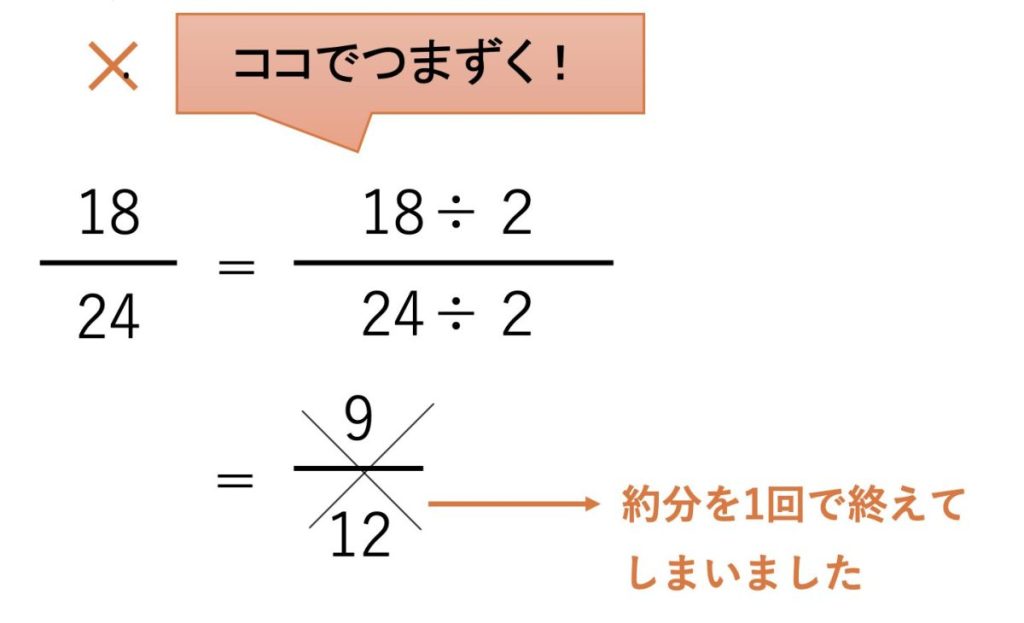
分数でつまずきやすいのはココ!
⚫︎約分を1回で終えてしまう
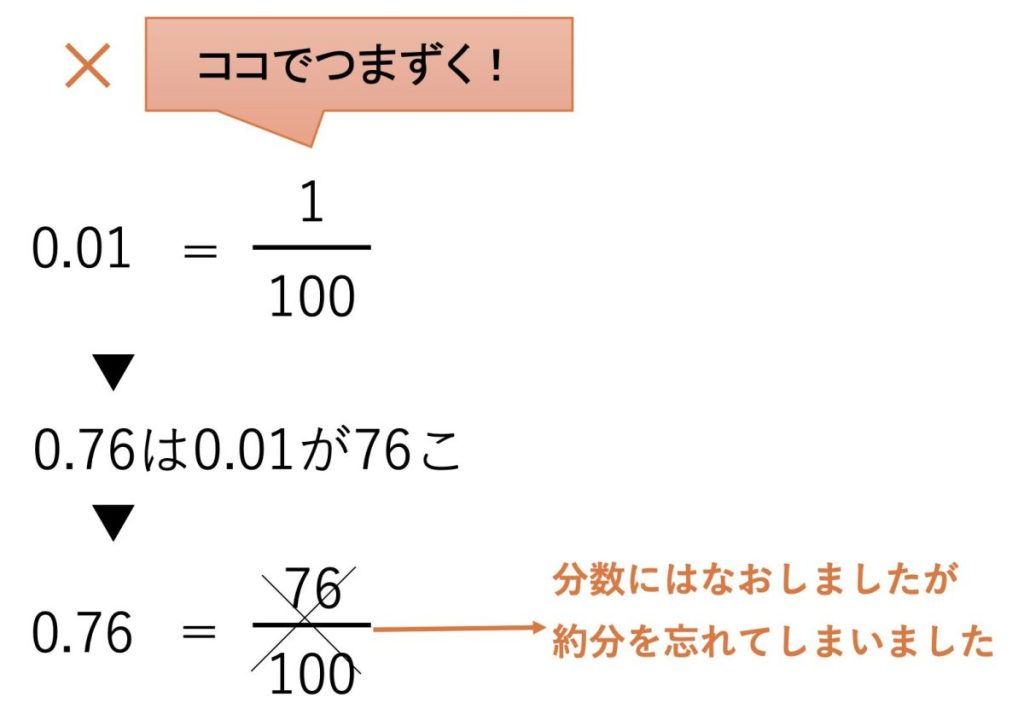
⚫︎小数から分数に直したあと、約分を忘れてしまう
子どもは楽しいとやる気になる。クイズも大好き
親がクイズ形式で子どもに質問していくのも効果的です。たとえば、
「27になるかけ算の組み合わせは?」
「48になるかけ算の組み合わせは?」
といった問題を出すことで、子どもは自然とかけ算の組み合わせを覚えることができます。
市販の教材でも、表に「48」、裏にその答えになるかけ算がずらりと載っているカードがあります。そういったカードを使って、楽しく学ぶのも良い方法ですね。遊び感覚で繰り返し取り組むことで、子どもの計算力を自然に鍛えることができます。
低学年で見直すチャンスを逃さないで
「学校に任せていればいずれできるようになるだろう」と放置してしまったり、「学校のテストで合格点を取っているから大丈夫だろう」と安心してしまったりすることはありませんか?
その時はできていても、本当にわかっているのかを確認しておいたほうがよいでしょう。
特に、2年生や3年生くらいの時期を逃さないでください。できていて当たり前と過信せずにノートやテストをチェックし、後々困らないように備えておくことが必要です。そのひと手間をかけるかどうかで、子どもの学力に大きな差が出ることもあります。
算数のつまずきをスッキリ解決!算数克服術がたっぷり詰まった1冊

算数でのつまずきは、原因を明らかにすることが克服の第一歩。2023年4月に発売した『算数嫌いな子が好きになる本 増補改訂版』では、「なぜ?」「どこで間違えた?」をしっかり振り返りながら、誤答例とあわせて、プロが算数克服術を伝授してくれます。今回、記事で紹介したチェックシートや暗算力アップの問題、つまずきやすいポイントも、こちらの本書から一部を紹介しています。
大人気の花まるグループ スクールFCの松島伸浩先生による、わかりやすい解決策を知ったら、お子さんも算数好きになるかも!
『算数嫌いな子が好きになる本 増補改訂版』詳しくはこちら>>
算数のつまずきを解決するならこちらもおすすめ

教えてくれたのは…

1963年生まれ。現在、スクールFC代表兼花まるグループ常務取締役。教員一家に育つも、私教育の世界に飛び込み、大手進学塾で経営幹部として活躍。36歳で自塾を立ち上げ、個人、組織の両面から、「社会に出てから必要とされる『生きる力』を、受験学習を通して鍛える方法はないか」を模索する。その後、花まる学習会創立時からの旧知であった高濱正伸と再会し、花まるグループに入社。のべ10,000件以上の受験相談や教育相談の実績は、保護者からの絶大な支持を得ている。『中学受験 親のかかわり方大全』『中学受験 物語ですらすら頭に入る よく出る漢字720』(実務教育出版)、『算数嫌いな子が好きになる本 小学校6年分のつまずきと教え方がわかる』(カンゼン)など著書多数。
*記事内の図や式は『算数嫌いな子が好きになる本 増補改訂版』(高濱正伸監修/松島伸浩著、カンゼン刊)を参考に掲載しているものです。
取材・文/黒澤真紀





