2年生は図形や容積など大事な単元が目白押し!
2年生になるとかけ算、三角形と四角形、長さの単位や容積(水のかさ)、10000までの数など、大事な単元が目白押しです。ここでも式の意味や各単元の「それぞれの定義の理解」が何よりも大切になります。
定義って何のこと? どう声をかければいい?
例えば「三角形とは何か」を聞かれたときにお子さんは答えられますか? 「えーっと三つの角と頂点が」「あれ?3つの辺が……?」と言葉に詰まってしまったら要注意。答えは「三角形は3つの点を線でつないだ図形」で、これが定義です。
言われたら「そうだった」と思っても、定義はいつのまにかあやふやになってしまいます。2年生で出てくるのは「頂点」「辺」角度は「直角」です。その一つ一つの意味を言えるかどうかを聞いておくと、子どもの中に残っているかどうかを見ることができますね。
この先の図形の学習ですが、3年生が三角形の性質、4年生が四角形の性質、5年生の面積とつながっていきます。そのときにここで学んだ定義もしっかり残っていないと、性質のところで混乱してしまうので、すごく大事なのです。
もちろん子どもに「定義を覚えなさい」とは言いません。「三角形ってどんな図形のことだっけ?」「四角形はどんな図形? じゃ、これって四角形なの?」「頂点て何のこと?」「辺は?」など聞いたり、「じゃあこれも四角形?」と親子で描いてみるといいですね。

かけ算は「式の意味」を知ることで文章題に強くなる
かけ算も同じように考えます。九九を暗記することも大事ですが、「かけ算とは(ひとつ分)×(いくつ分)」を表す計算だと常に頭のどこかにおいてほしいですね。なぜならここでいう(ひとつ分)の発想は、「割合」の「もとになる数」の感覚につながっていくからです。2つの数字に対してどちらを「ひとつ分」「いくつ」にするかはいろいろな見方がありますが、自分が「ひとつ分を3」「いくつかを4」としたら「3×4」という計算になります。数字の意味はすごく大事ですね。
どの数を「ひとつ分」とし、どの数を「いくつ分」とするかは、問題や数字の見方によって変わりますが、「(ひとつ分)×(いくつ分)」の位置関係は固定で行くほうが、割合を学ぶときに混乱を防ぐことができますし、文章題が出てきたときにすっと式を立てやすくなります。
数直線の「目盛り」は読めていますか?
2年生で初めて登場する図が「数直線」。それまでは具体的な絵をかきながら理解していた問題の意味を、少しずつ抽象度を上げながら図にして簡単に考えられるように学んでいきます。
はじめのうちは「1目盛りを1」として学びますが、数が大きくなってくると1目盛りの数が変わります。「100ずつ増えているからこの目盛りは50だ」と気づければ大丈夫ですが、間違えるようであれば、1目盛りの読み方を一緒にたどってあげてください。
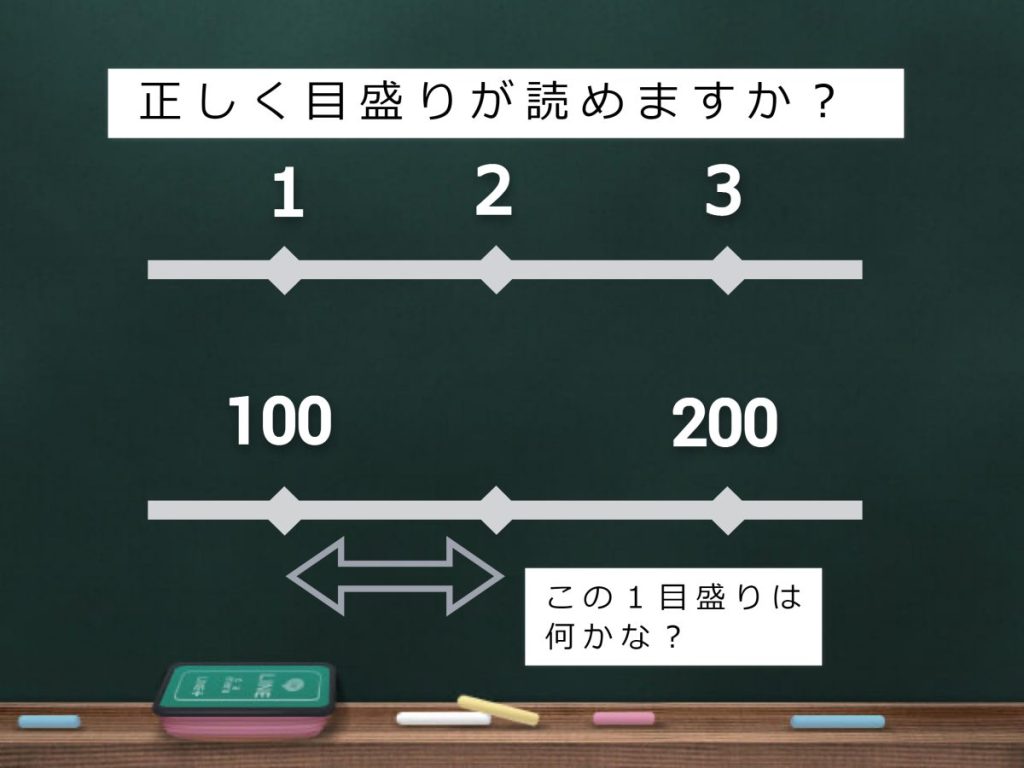
「1目盛り」を捉える習慣があると、のちの「割合」で「もととなる数」「1あたりの数」などを考えるときに生きてくるので、重要な確認ポイントになります。先ほどから「割合」につながる話が多く出てきていますが、小学生全体で考えると5年生の「割合」は算数の鬼門。5年生になって「割合でやられた」と混乱することを防ぐため、低学年のうちから少しずつ算数感覚を身につけてほしいなと思います。
算数とは「意味・しくみ」と「テクニック」を掛け合わせた教科
2年生の算数の振り返りポイントをお伝えしました。はじめに算数は「知識をつなげて新しい知識を生み出す教科」と言いましたが、具体的に言うなら「定義の積み重ね」と「計算テクニック」と掛け合わせた教科ということになります。
簡単な時期だかこそ、テストの答えが〇であっても、確実に頭に入っているか、関わり方の参考にしてみてください。
1年生の算数、年度末復習についてはこちら

記事監修






