2桁のかけ算に使えるインド式計算法とは?
2桁のかけ算を暗算するには、インド式の計算法が便利です。まずは、インド式の計算における考え方を簡単に解説します。
効率よく答えを導き出す計算法
インド式計算法の大きな特徴は、効率よく答えを導き出す考え方にあります。たとえば36×25という問題が提示された場合、インド式の計算法では「計算しやすい形に分解できないかな」と考えます。つまり、2桁×2桁のままで暗算しようとはせず、計算しやすい2桁×1桁や1桁同士のかけ算の形にするのです。
36×25の場合だと、36×(5×5)という2桁×1桁×1桁の形に分解できます。それでも暗算が難しい場合は6×6×5×5の形に分解し、順番を入れ替えて6×5×6×5とするのも手です。6×5=30なので、30×30を暗算して答えは900だとわかります。
インド式の計算法のメリット
インド式の計算法には、計算速度が速くなるという大きなメリットがあります。特に、かけ算や割り算といった複雑な計算を短時間で処理できるのが特徴です。たとえば99や101のように100に近い数字のかけ算は、一般的な筆算よりもはるかに効率的に計算できます。これにより、インドの学生たちが数学オリンピックで優れた成績を収めている背景にもなっています。
さらに暗算力が自然に身に付くため、日常生活でも素早く計算できるようになります。これにより計算ミスが減り、自信を持って数学に取り組むことができるのもメリットです。実際に計算が速くなると数学に対する苦手意識が減り、学習意欲が向上することも。加えて数字のパターンや組み合わせを理解する力が養われるため、数学の応用力も自然と高まります。
インド式の計算法のデメリット
一方で、インド式の計算法にも注意が必要です。まず、基本の計算力がないと効果が十分に発揮されない点が挙げられます。インド式は計算を効率化するためのテクニックであり、基礎的な計算力が前提となります。そのため、基本の筆算をしっかり身につけてから挑戦することが大切です。またインド式は独自の計算アプローチが多く、最初は慣れるまで時間がかかることも。日本で一般的に教えられる計算法とは異なるため、最初は混乱することもあるでしょう。
また暗算に頼る場面が多く、途中の計算過程が省略されやすいため、計算ミスが起きた際に原因を特定しにくいというデメリットもあります。さらにインド式の計算法は特定のパターンに強い一方で、あらゆる計算に適用できるわけではないため、使いどころを見極める必要があります。
パターン別・2桁のかけ算の暗算方法
問題パターンによっては、数の法則を使って暗算できる場合もあります。4つのパターンで使える暗算方法をチェックし、スムーズな計算に役立てましょう。
100に近い数同士を掛ける場合
たとえば95×97の場合、100との差を使って暗算できます。暗算の流れは以下の通りです。
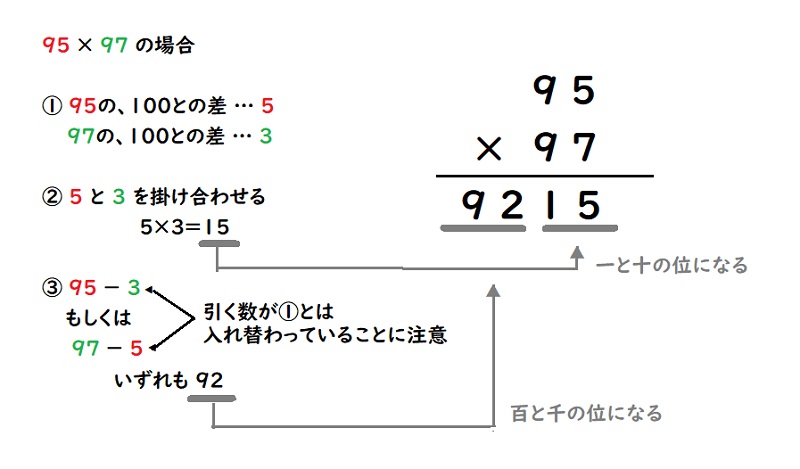
①それぞれの数字から100との差を求める
100から、それぞれ95と97を引くと、5と3
②100との差同士を掛けた数を出す
100との差同士を掛けた5×3=15が一の位・十の位の答えとなる
③百の位・千の位を求めるために95から3(97のほうの100との差)、もしくは97から5(95のほうの100との差)を引く(引く数は、足し算のもう一方の数の100との差であることに注意)
95から3を、もしくは97から5を引いた数(どちらも同じ数になる)が百の位・千の位になる
ここではいずれも92になるため、答えは9,215です。
11〜19の数同士を掛ける場合
13×16のように20に満たない数同士のかけ算では、以下のような流れで暗算します。
①片方の数を分解する
16を10と6に分解
②分解した数のうち少ない方をもう片方の数へ移動させる
10と6のうち6を13に移動させて計算すると(13+6)×10=190となる
③一の位の数同士を掛ける
13と16の一の位の数を掛けると3×6=18
④合計する
190+18=208
なお、16の6を13に移動できる理由は、下の面積図を見ると理解しやすいでしょう。
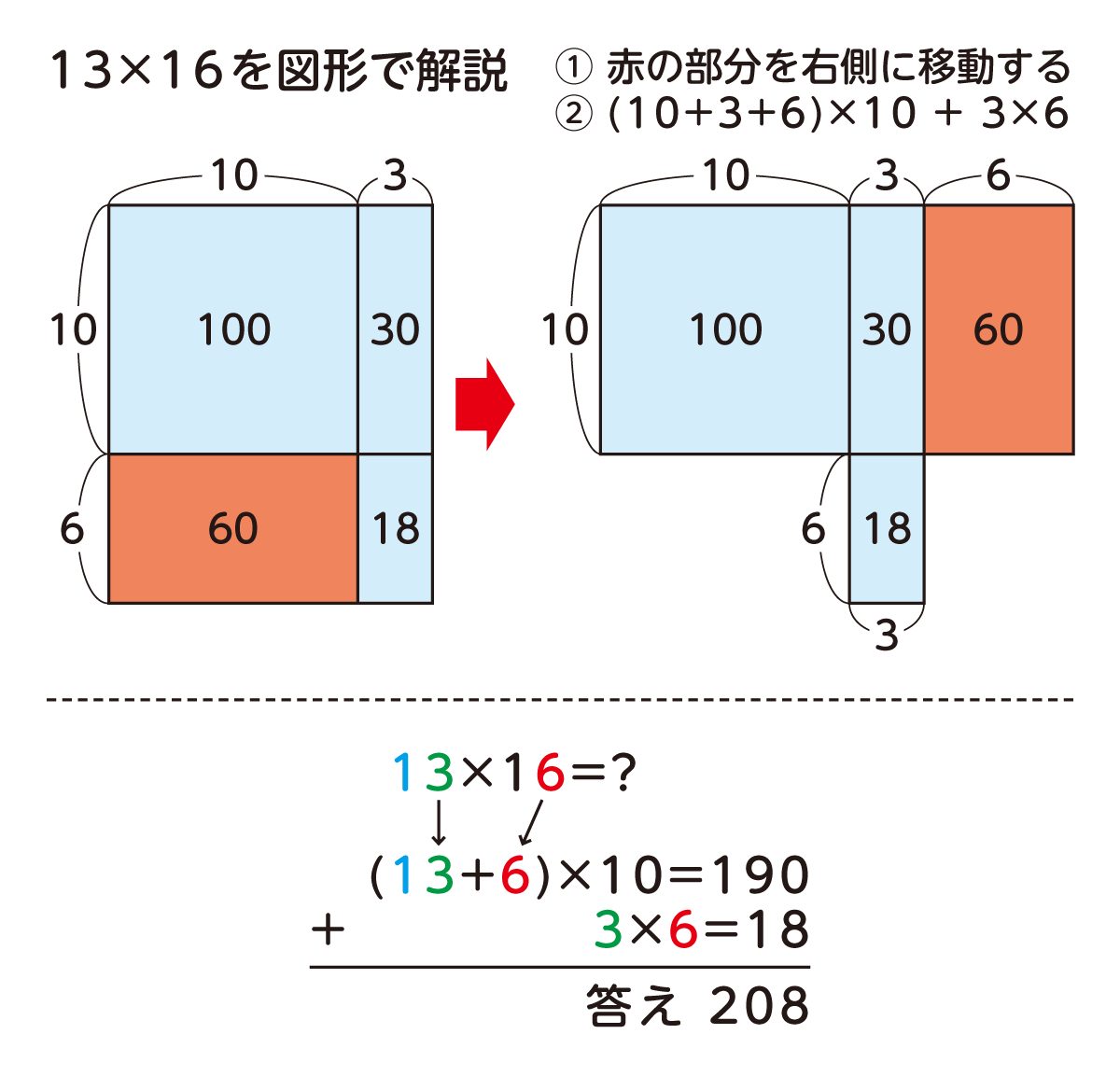
13×16cmの長方形だとすると、16cmの6cm分を移動させて、13cmの延長上に加えるイメージです。すると、長方形の面積は19×10cmになり、追加できなかった3×6cmの面積が余ります。そのため、片方を10にして計算した後で一の位の数を掛けた答えを足す必要があるのです。
十の位が同じ・一の位の合計が10の場合
42×48のように、十の位が同じかつ一の位の合計が10の場合には、以下のような順番で暗算できます。
①それぞれを一の位・十の位に分解する
(40+2)×(40+8)
②片方の一の位を、もう片方に加える
42の2を48へ加えて計算すると40×(40+2+8)=40×50=2,000
③一の位の数同士を掛ける
42と48の一の位の数を掛けると2×8=16
④上記の答えを合算する
2,000+16=2,016
それぞれの数を一の位・十の位に分解するのは、下の図のような四つの長方形に分けるイメージです。
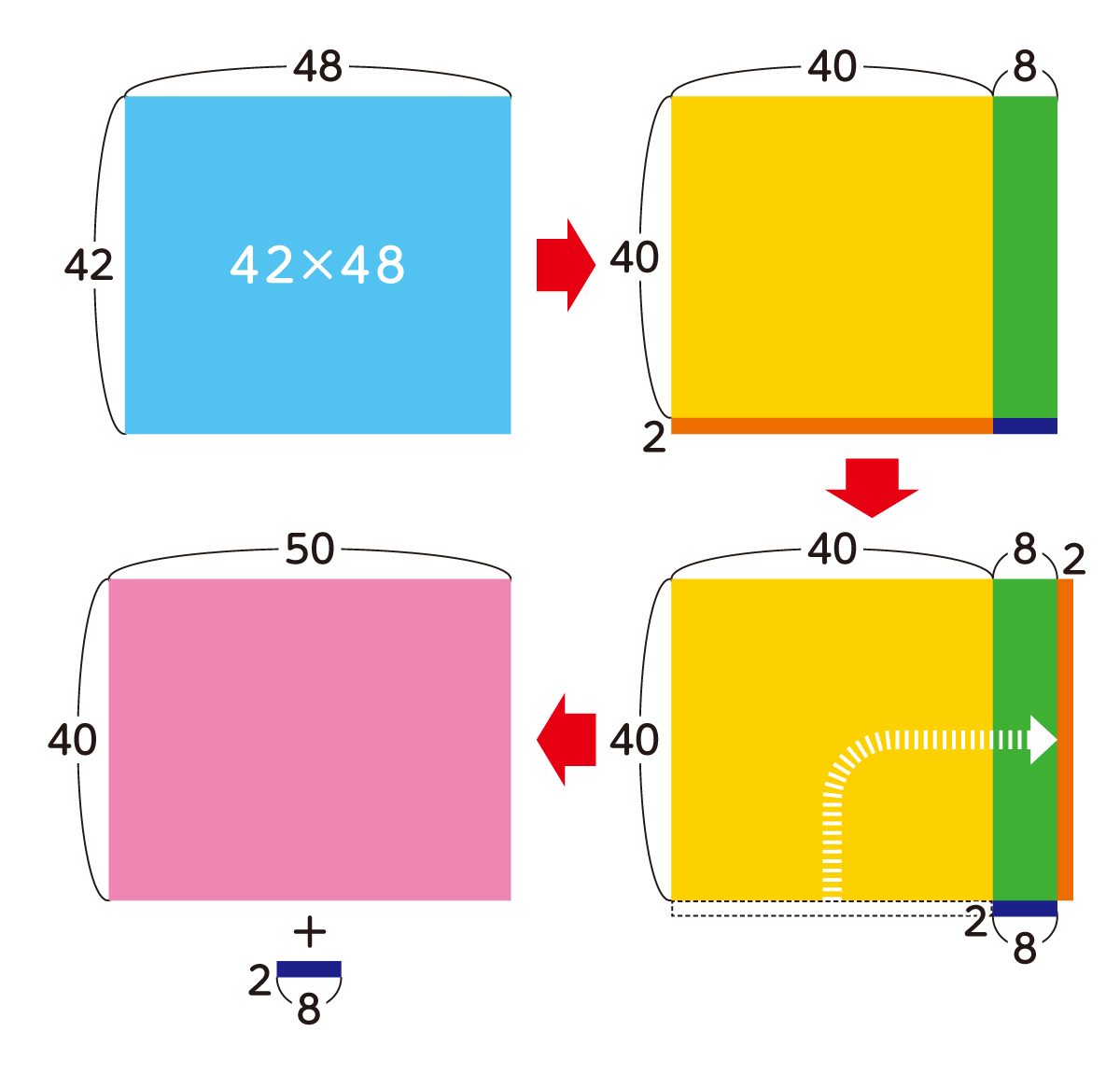
2×40cmの長方形(図のオレンジ色部分)の向きを変えると、40×8cmの長方形の隣にぴったりと収まります。結果的に、40×50cm(40+8+2)の長方形と、2×8cmの長方形に分かれます。そのため一の位の数同士を掛けた16を追加し、答えは2,000+16=2,016となるのです。
十の位が同じ・一の位の合計が10でない場合
「十の位が同じ数・一の位の合計が10の場合」を応用すると、一の位の合計が10ではない2桁のかけ算も暗算できます。
66×65を例にして考えると、一の位の6と5を6と4と1に分ける形です。このように一の位の合計が10になるように数を分けると、66×(64+1)となり66×64+66×1の計算式が成り立ちます。
66×64の答えは前述の方法を使うと60×(60+6+4)=60×70=4,200に6×4=24を足した4,224です。4,224に残りの66×1=66を加え、4,290だとわかります。
パターンに当てはまらない場合の暗算方法
条件に合わない2桁同士のかけ算でも、基本の考え方をおさえておくことで暗算が可能です。2種類の暗算方法をチェックしましょう。
たすき掛けで求める方法
複雑な2桁同士のかけ算でも、たすき掛けを使って以下のように考えると答えを導き出せます。例として55×74で計算してみましょう。
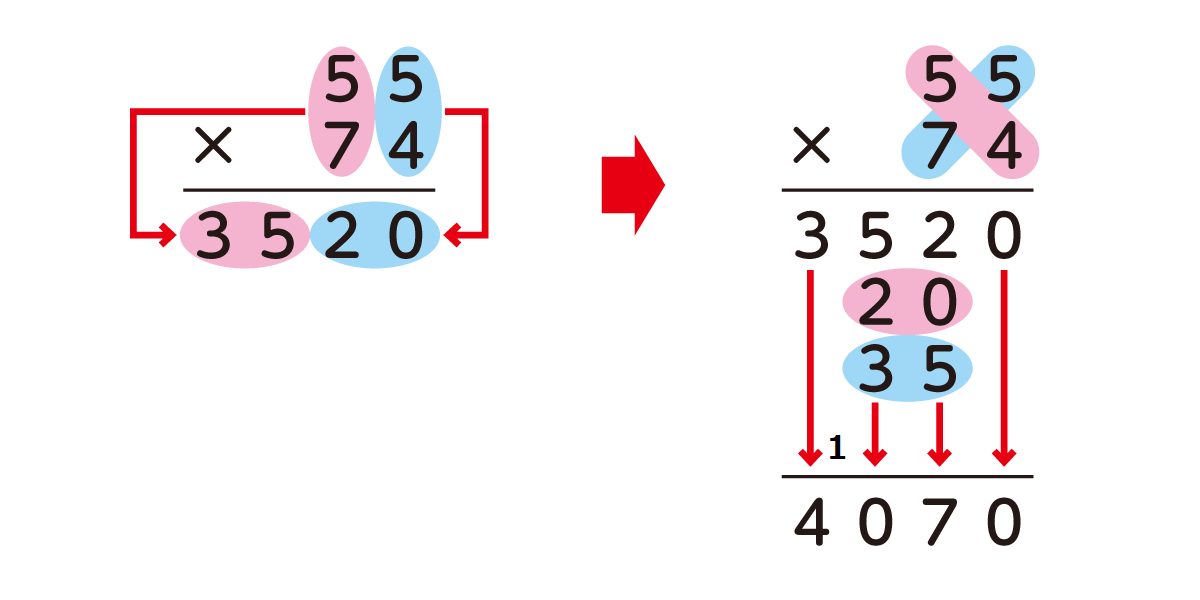
①一の位・十の位の数同士をそれぞれ掛ける
一の位同士を掛けると5×4=20
十の位同士を掛けると50×70=3,500
合計した数は3,520
②一の位の数と十の位の数をそれぞれたすき掛けする
55の50と74の4を掛けた50×4=200が一つ目の答え
55の5と74の70を掛けた5×70=350が二つ目の答え
③上記で導き出した数を合計する
3,520+200+350=4,070
上記の方法で暗算をする場合、位取りに注意しましょう。たとえば74の7は10が七つあることを示しているため、7ではなく70として計算するのが正解です。
※上の図はわかりやすくゼロを省略してあります。
切りのよい数に直す方法
計算が苦手な人には、切りのよい数に直す方法もおすすめです。
たとえば48×82の場合だと、82を80と2に分けて考えます。すると48×(80+2)になるので、48×80と48×2をそれぞれ暗算すると3,840+96の式が成り立ちます。
ただ、96のままだと暗算しにくいため、100-4の形に直すのがポイントです。3,840に100を足した3,940から4を引いた3,936が答えだとわかります。
よくある質問
2桁のかけ算は、小学生がつまずきやすい単元のひとつです。学年が上がるにつれて計算のステップが増えるため、「いつ習うの?」「どう教えればいい?」と悩む保護者の方も多いもの。ここでは、よくある疑問についてお答えします。
Q. 2桁×2桁のかけ算は何年生で習う?
一般的には小学4年生で学びます。3年生で九九や筆算の基礎を身につけ、その応用として2桁同士のかけ算に進みます。
Q. 繰り上がりのあるかけ算の教え方のコツは?
ポイントは「位ごとに分けて考える」ことです。まず一の位同士をかけ算 → 繰り上がりをメモ → 次に十の位をかけ算、と順番をはっきりさせると理解しやすくなります。途中の計算をノートに書き残す習慣をつけると、ミスも減ります。
Q. 暗算が苦手な子へのアプローチ方法は?
暗算が苦手な子には、視覚的なサポートが効果的です。ブロックや図、数直線を使って「数のまとまり」をイメージさせると理解が深まります。また九九の反復練習をゲーム感覚で取り入れると、計算の土台が安定しやすくなります。
テクニックを知り2桁のかけ算を暗算しよう
インド式の考え方をすると、一見すると難解な2桁のかけ算でも筆算や電卓を使わずに計算できます。インド式の計算をするポイントは、わかりやすい形に直せないかを考えてみることです。
算数は答えが明確に決まっているものの、正解へたどり着くまでの考え方は一つとは限りません。持っている知識を駆使して複雑な計算式をわかりやすい形にするのは、パズルを解くような楽しさもあります。買い物や子どもの宿題などで2桁のかけ算に遭遇した際には、暗算テクニックを使って答えを出してみましょう。
こちらの記事もおすすめ
構成・文/HugKum編集部