【小5算数 速さ】子どもがつまづくのは公式。元教師が教える、公式図で解決する方法！

「公式」を覚えるときに、つまづきやすい

５年生の算数の学習のひとつに「速さ」の学習があります。子どもは、式を立てるときにつまづきます。

かけ算をするのか、わり算になるのか、距離を時間で割るのか、速さで割るのかなどで、混乱します。

「速さ」の問題は、公式を表した円形の図に当てはめて解く

問題を解くときに必要なのが「公式」です。線分図、面積図などにして解くこともできますが、「公式」に当てはめれば解けます。

まずは、子どもに「公式」を覚えさせてしまいましょう。
円の中に、「速さ」「時間」「距離」を書いた図を使うと覚えられます。

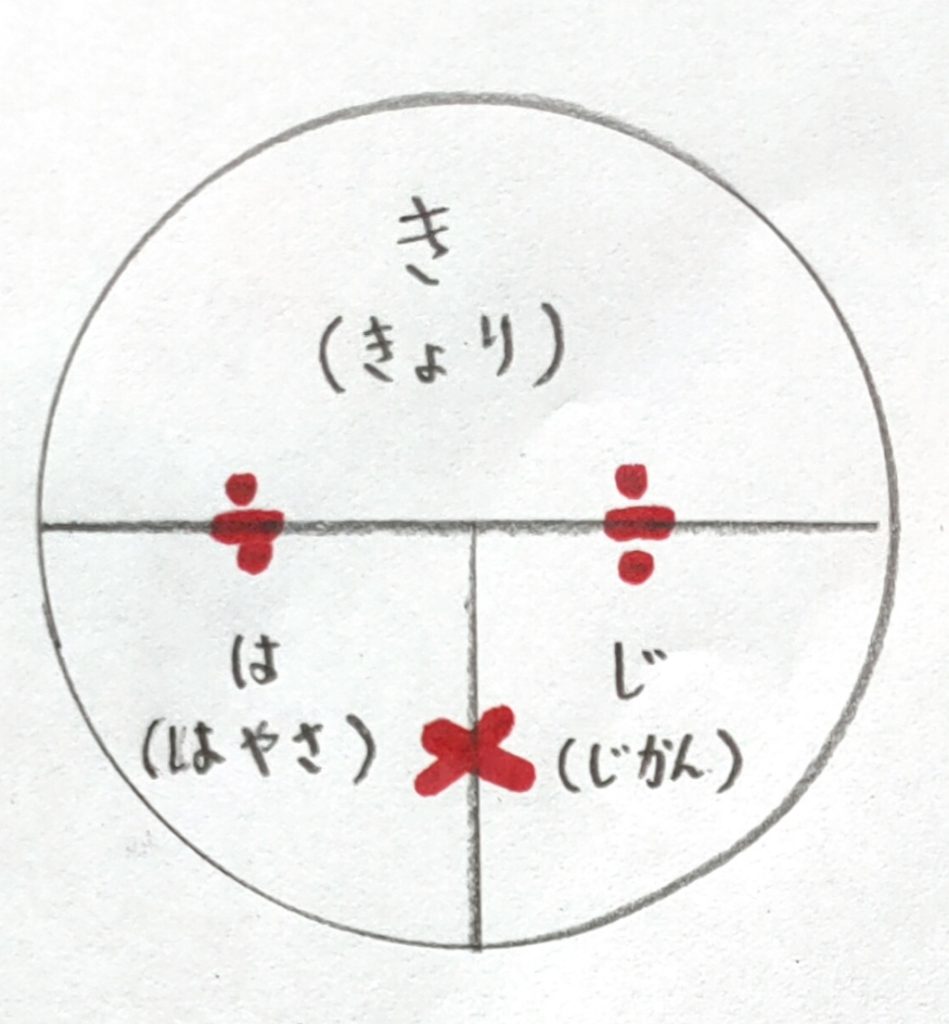
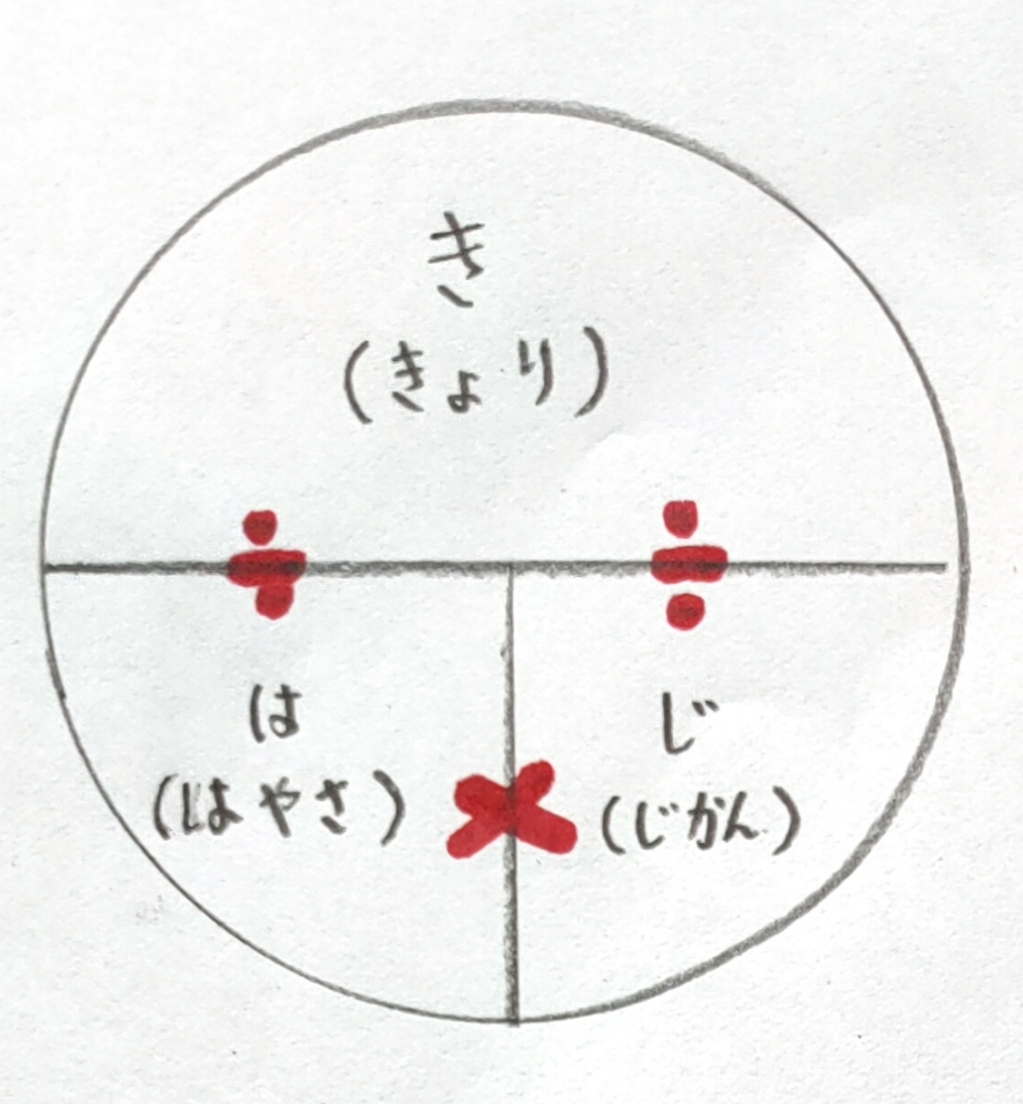
公式の図の書き方

①「はじき」と左はしから「反時計回り」に書かせる。
※「（お）はじき」と、ごろ合わせのようにすると覚えやすくなる

②図のように「×」「÷」の記号を書くと、公式が見えてくる。

③この図の書き方を覚えておけば、公式を覚えたことになる。

・速さ×時間＝距離

・距離÷速さ＝時間

・距離÷時間＝速さ

と、なる。

「距離」の部分が「道のり」になっているときは「速さ×時間＝道のり」のように、距離を「道のり」に変えるだけでいい。
※距離は、Ａ点とＢ点を直線で結んだ長さ。道のりは、実際に移動した距離

できるようになることが大切

「公式を覚えさせよう」と言うと、「意味を理解させる」ほうが大切だと主張する方が出てきます。意味を学習させるのも悪いことではありません。ただ、世の中には「意味が分かる」よりも「できることが大切」ということも多くあります。

たとえば、パソコン。どんな仕組みになっているのか分からなくても使えます。パソコンの仕組みを理解してから使う人は、少ないでしょう。「速さ」の学習もゴールは、「問題が解ける」こと。とりあえずは、公式を覚えて、問題が解けるようになればいいのです。

公式を表した図を使って、例題を解いてみる

次の３問を「公式」を示している図に当てはめて解いてみましょう。

基礎編１

①何を求める問題か、とらえさせます（「距離」を求める）。

②「速さ」「距離」「時間」の単位がそろっているか確認させます。

③図の公式に当てはめます。　速さ×時間＝距離

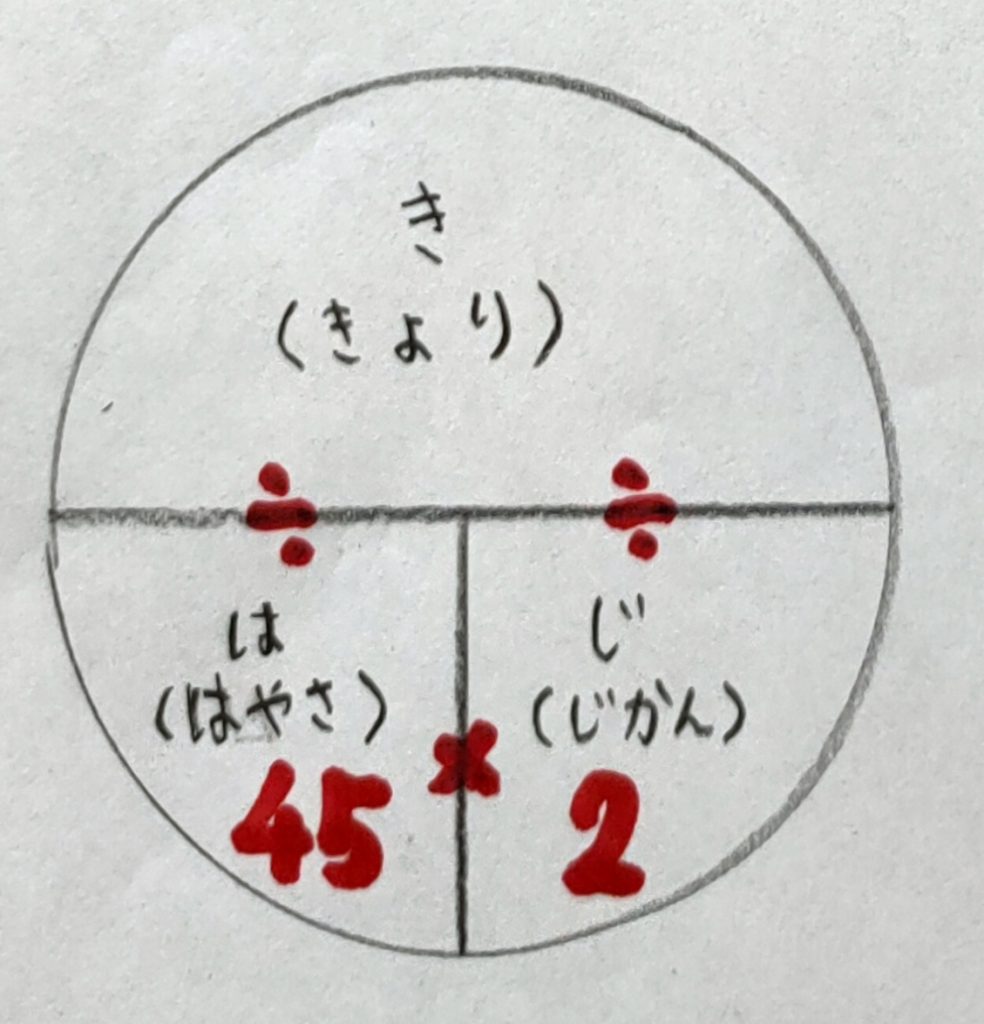
④式と答え
４５×２＝９０

答え　９０㎞　となります。

基本編２

①何を求める問題か捉えさせます（「時間」を求める）。

②「速さ」「距離」「時間」の単位がそろっているか確認させます。

③図の公式に当てはめます。
距離÷速さ＝時間

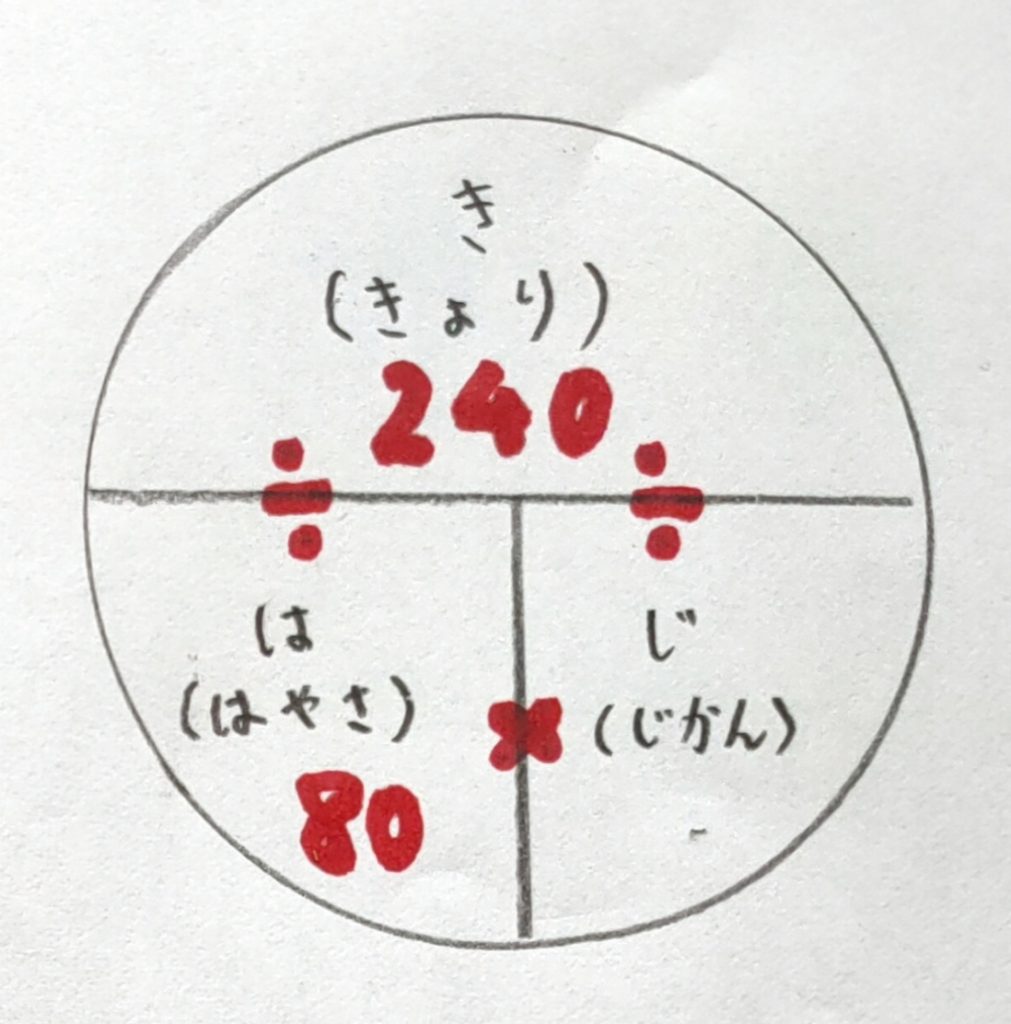
④式と答え
２４０÷８０＝３

答え　３時間

応用編

①何を求める問題か捉えさせます（「速さ」を求める）。
ＡとＢ両方の「速さ」を求めないといけない問題ですが、解き方は変わりません。公式に当てはめて、計算します。

②「速さ」「距離」「時間」の単位がそろっているか確認させます。

③ＡとＢ、それぞれを図の公式に当てはめます。
距離÷時間＝速さ

Ａ

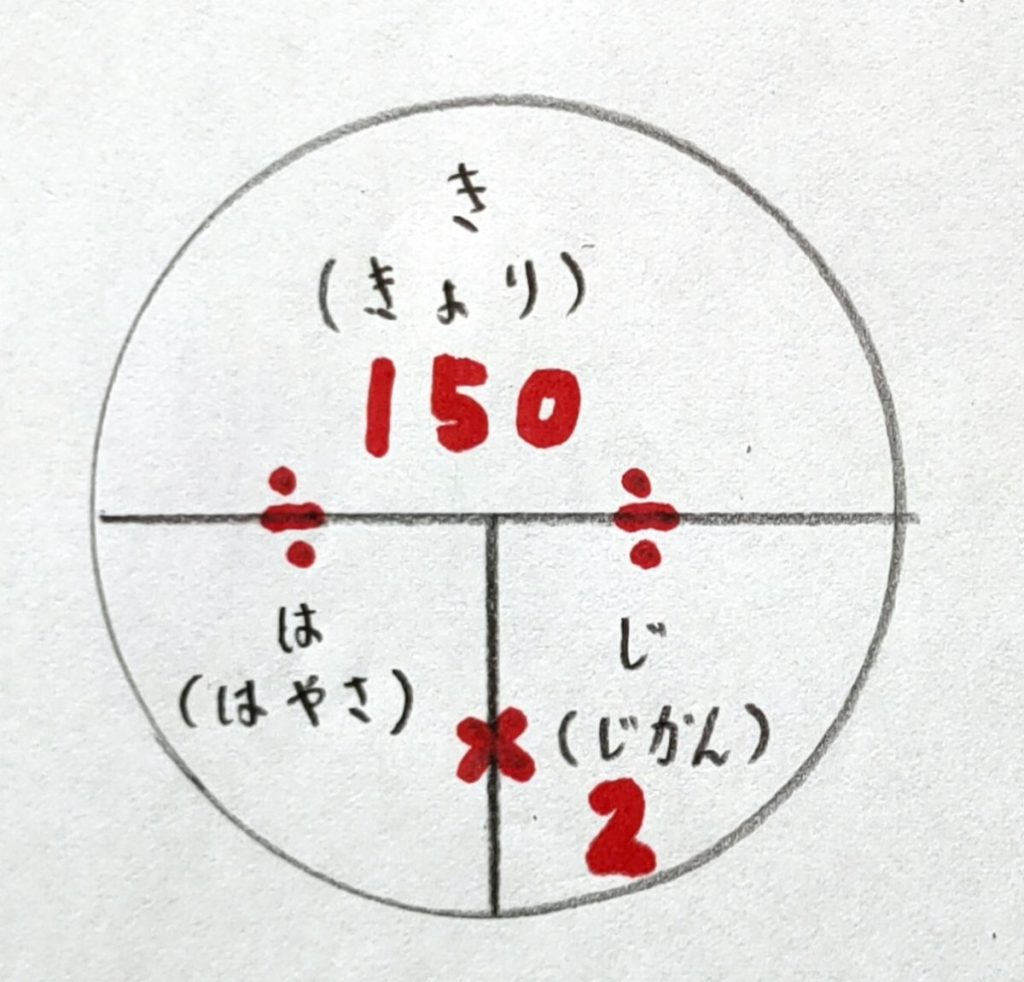
Ｂ

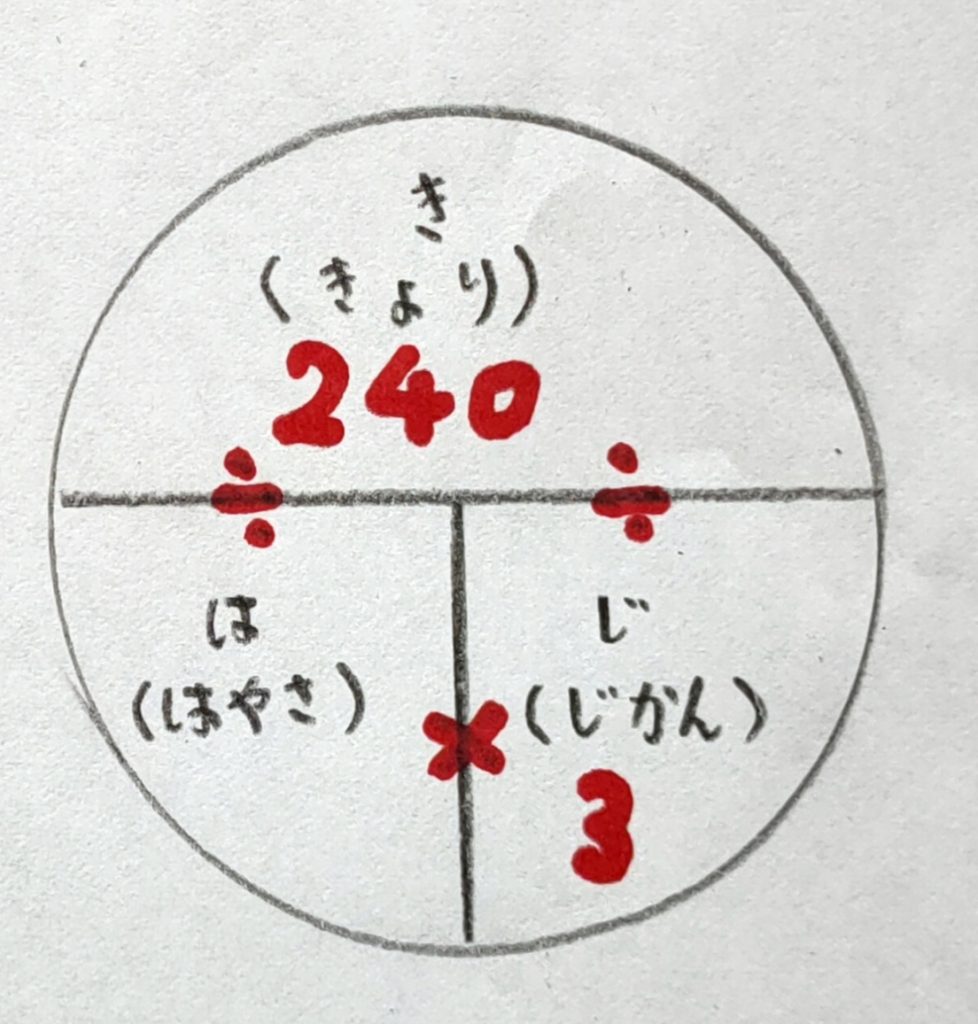
④式と答え

Ａ →１５０÷２＝７５　１時間で７５㎞走る

Ｂ→ ２４０÷３＝８０　１時間で８０㎞走る

答え　Ｂの自動車のほうが速い

お家の人から子どもへのアドバイスのポイント

私が「速さ」の授業をしていたときのことです。「ゲーム」を通して教えた時期がありました。教室にいくつかミニカーを持ち込み、どのミニカーが速いのか競走させ、授業をしました。

子どもは喜んでいました。授業後のアンケートにも多くの子が「楽しかった」と書いていました。当時は『「速さ」を出すにはどうすればいい？』などと考えさせていましたが、テストの結果はよくありませんでした。ミニカーの競争で楽しい授業になり盛り上がりましたが、問題が解けるようになるかどうかとは、別だったのです。

結局は、公式をしっかり覚えていないと解けないのです。

公式を覚え、単位がそろっているかどうかに気をつければ、解けるようになります。アドバイスのポイントは、公式を覚える円形の図（はじき）を教えることです。

あとは、今まで書いてきた手順で問題を解くことを教え、慣れていけばよいでしょう。

あなたにはこちらもおすすめ

これなら書ける！ 元小学校国語教師が教える「遠足・学習発表会の作文」の書き方。基本は「材料集め」→「構成」→「書く」の３ステップ。

国語教師が「作文」の書き方をレクチャー という私も、小学生のときは「作文」が嫌いでした。 「そして遊びました」「それから寝ました」と...