
小学生の算数では計算から図形まで幅広い単元を学習します。前回の記事では、小学1~3年生の子どもたちが特につまずきやすい単元について解説しました。今回は、前回の続きとして4~6年生で習う単元について、子どもたちが特につまずきやすい単元を解説していきます。
目次
4~6年生が最もつまずきやすい単元はどれ?
まずはクイズ形式で予想してみましょう。小学4~6年生の学習範囲で、最もつまずく子が多い単元は次のうちどれだと思いますか?
①約分と通分
②角度の計算
③およその数・四捨五入
一般的なイメージでは、複雑な「約分と通分」が最も難しそうだと思われているようですが、正解は①ではありません。実は、最もつまずく子が多い単元は「③およその数・四捨五入」です。皆さんの予想はいかがでしたか?
最もつまずきやすいのは「およその数・四捨五入」

「およその数・四捨五入」は4年生で学びます。前段階で億・兆の位を扱う大きな数を学んだあと、がい数(概数)で考える方法を学んでいくのです。
この単元は、4年生から中学生にかけて学ぶ「平均」「数列」「べき乗」など、数の概念を考えるための入り口となる単元です。
ここでつまずくと、「平均」「数列」など後に続く単元が軒並み苦手になってしまいます。それだけ重要度の高い単元でもあるのです。
およその数・四捨五入でつまずく原因は?
およその数・四捨五入でつまずく原因は、「最初の教わり方が少し悪かった」というような“ちょっとしたきっかけ”が苦手の始まりになるパターンがよくあります。
大きな桁に数字が並ぶ問題が多いため、ちょっとした苦手意識から「解くのが大変そう」「難しそう」「面倒くさそう」といったイメージを持ってしまい、その後は本来なら解けるはずの問題も取り組む気力を失くしてしまう……という悪循環になってしまうのです。
また、重要度の高い単元であるにも関わらず、桁の大きな数をがい数で考えるという作業は、小学生の日常生活と強く結びつくものではないため、なかなかイメージしにくいというのも苦手の原因になっています。
イメージしにくい大きな数を直感的に理解するためには、やはり低学年の段階で「位の概念」をしっかり理解しておくことが必要になります。
低学年で習う算数の単元で「位の概念」の理解は最も重要であること、重要であるにも関わらず最もつまずきやすい単元であることは前回の記事でお伝えした通りですね。高学年になっても、ここが全ての根っこになっていることがお分かりいただけるのではないでしょうか。
▼前回の記事はこちら

およその数・四捨五入のつまずきを克服するためには?
およその数・四捨五入のつまずきを解消するにはどのような方法があるでしょうか。すでに苦手意識がある、つまずきを感じているというお子さんは、まず学年を超えて「位の概念があやふやでないか?」をチェックしてみることをおすすめします。
位が分からないままでは四捨五入は絶対にできるようにならないので、まずは位の理解を最優先にします。位さえ理解できていれば、「およその数・四捨五入」の問題は計算そのものが難しいわけではありません。
少しの苦手意識が尾を引く単元になりますので、傷口が小さいうちに早めに対処することがつまずきを克服する秘訣です。

およその数が使えるだけで、テストの点数がアップする!?
およその数・四捨五入は、「テストの見直し」にも役立ちます。自分で解いた答えが合っているかを確かめる検算をするとき、およその数を使って大体の数字が合っているか見当を付けますよね。つまり、およその数が使えるということは、テストの見直しも楽にできるということです。この単元を理解しておくことは、算数・数学のテスト全体の得点力UPにつながりますよ!
2番目につまずきやすいのは「角度の計算」
次につまずきやすい単元は「②角度の計算」です。この単元は、図形の理解と計算力、どちらも必要とする単元です。
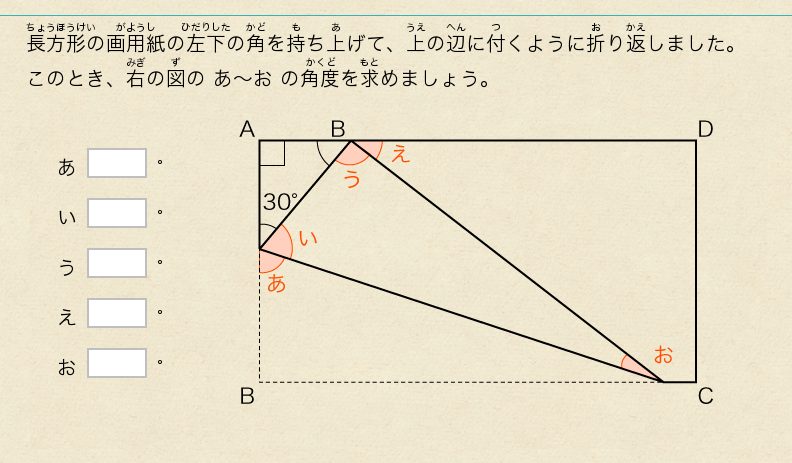
「角度の計算」は、どうしてつまずきやすい?
角度の計算の難しさは、示されている角度と図形をよく見て、すでに角度がわかっている箇所を自分で探して見つけなくてはならないところにあります。
計算ドリルのような問題は、最初から計算式が書かれているため答えを出すだけで良いのですが、角度の計算では、計算式そのものを自分で導き出す必要があるのです。
また、図形から計算に必要な角度を見つけていく作業になるので、数字を書き入れたり補助線を引くなどして手を動かさなくては答えに辿りつけません。特に、普段からスピード勝負の計算問題を中心に学習に取り組んでいる子は、頭の中で計算を完結することに慣れているため、手を動かして数字を拾う作業が苦手だったりします。計算の得意な子が「角度の計算」になると急につまずくのは、このような原因があるからです。
「角度の計算」のつまずきを克服する方法は?
角度の計算について、つまずきを解消するには「どれだけ図形の中に三角形や四角形を見つけられるか」がポイントになります。
まずは図形をしっかり見て、すでに示されている角度を確認します。そこから、いかに分かる角度を見つけられるかがポイントになるので、とにかく手を動かして、分かる角度をどんどん書き込んでいくことが大切です。

頭で完結しようとせず、角度の問題は常に手を動かして書き込んでいくことを癖付けましょう。また、角度の問題は「慣れ」も大切な要素です。何度か解くうちに「こうすれば答えに辿り着ける」というパターンが見つかりますから、ちょっとした謎解きゲームの感覚で、楽しみながら色んな問題にチャレンジしてみてください。
難しそうなイメージの「約分と通分」は3番目という結果に
最後に残ったのは「①約分と通分」です。一般的には3つの単元の中で最も難しく、つまずきやすいというイメージがあるようですが、RISU算数を利用している子どもたちのデータでは「そこまでつまずかない」という結果が分かりました。
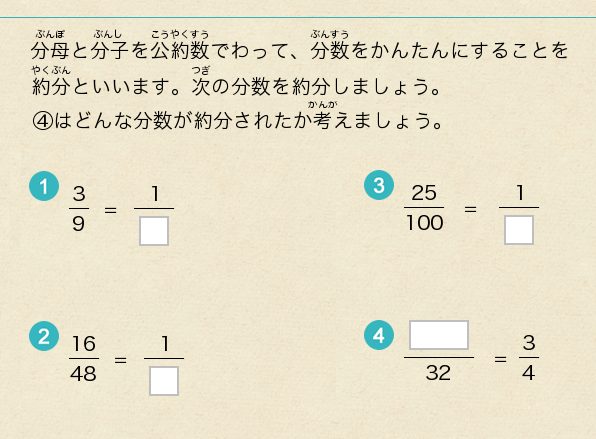
「約分と通分」でつまずく原因は?
もし「約分と通分」でつまずきを感じるのであれば、前段階の知識である「素数」や「因数分解」の理解があやふやなことが原因として考えられます。
小学校では「倍数」「約数」を5年生になってから学習します。その延長上で「素数」や「因数分解」が登場しますが、塾では4年生ぐらいから学習を開始するにもかかわらず、学校の授業ではサラッとしか触れていないことも多く、通分と約分の基礎になる概念が分からないままになってしまいます。
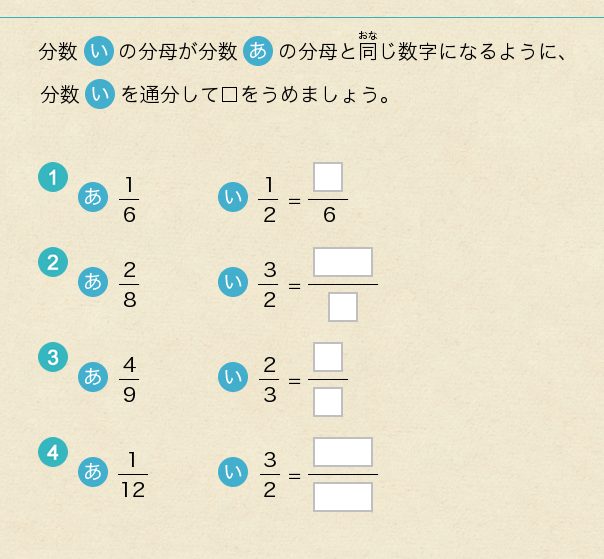
「約分と通分」のつまずきを克服する方法は?
理屈が分かれば解けるタイプの子であれば、倍数や約数の仕組みをかみ砕いて、しっかり説明してあげるようにします。約分・通分とどう関わっているかが分かれば、苦手意識はなくなるでしょう。
小学校での素数や因数分解の学習がサラッと進んで終わってしまったという場合は、「約分と通分」を学習する前にもう一度しっかり復習しておくことをおすすめします。急がば回れで、基礎になる概念を理解してから進む方が結果的に苦手克服の近道になります。
九九をきちんとマスターしているか?も大切なチェックポイントです。答えが12になるかけ算を2×6しか思いつかないよりも、パッといくつもの式を思いつくほうが有利ですよね。もし九九をマスターできていないようでしたら、九九の表をデスクに置きながらやるなどの工夫をして、まずは九九の苦手から克服しましょう。

位の理解は学年を超えて大切な最重要単元です!
今回は4~6年生で習う単元について、つまずく原因と克服方法をお伝えしました。1~3年生編も含め、大人が思う難しさと、子どもの視点で見た難しさは大きく違うことに気付かされる結果となりました。
4~6年生編で最もつまずきやすい結果となった「およその数・四捨五入」ですが、この単元のつまずきの原因は、結局は「位の理解が不十分」なことにつながります。そう考えると、低学年での「位の理解」は学年を超えて最も重要な単元であると言えるでしょう。算数は幅広い単元を学習しますので、今回の記事を参考に復習や実力チェックに活かしてください。
こちらの記事にも注目!

記事執筆

〈タブレット教材「RISU算数」とは〉
「RISU算数」はひとりひとりの学習データを分析し、最適な問題を出題するタブレット教材。タイミングの良い復習や、つまずいた際には動画での解説の配信を行うことにより、苦手を克服し得意を伸ばします。
期間限定のお試しキャンペーンはこちら≪
『10億件の学習データが教える 理系が得意な子の育て方』

構成/HugKum編集部






